2021

Vidéos
J. Fine - Knots, minimal surfaces and J-holomorphic curves
I will describe work in progress, parts of which are joint with Marcelo Alves. Let L be a knot or link in the 3-sphere. I will explain how one can count minimal surfaces in hyperbolic 4-space
D. Tewodrose - Limits of Riemannian manifolds satisfying a uniform Kato condition
Presentation of a joint work with G. Carron and I. Mondello where we study Kato limit spaces.
P. Burkhardt - Pointwise lower scalar curvature bounds for C0 metrics via regularizing Ricci flow
We propose a class of local definitions of weak lower scalar curvature bounds that is well defined for C0 metrics. We show the following: that our definitions are stable under greater-than-second
D. Stern - Harmonic map methods in spectral geometry
Over the last fifty years, the problem of finding sharp upper bounds for area-normalized Laplacian eigenvalues on closed surfaces has attracted the attention of many geometers, due in part to
M. Lesourd - Positive Scalar Curvature on Noncompact Manifolds and the Positive Mass Theorem
The study of positive scalar curvature on noncompact manifolds has seen significant progress in the last few years. A major role has been played by Gromov's results and conjectures, and in
J. Wang - Topological rigidity and positive scalar curvature
In this talk, we shall describe some topological rigidity and its relationship with positive scalar curvature. Precisely, we will present a proof that a complete contractible 3-manifold with
Y. Lai - A family of 3d steady gradient Ricci solitons that are flying wings
We find a family of 3d steady gradient Ricci solitons that are flying wings. This verifies a conjecture by Hamilton. For a 3d flying wing, we show that the scalar curvature does not vanish at
C. Li - Classifying sufficiently connected PSC manifolds in 4 and 5 dimensions
In this talk, I will discuss some recent developments on the topology of closed manifolds admitting Riemannian metrics of positive scalar curvature. In particular, we will prove if a closed PSC
D. Semola - Boundary regularity and stability under lower Ricci bounds
The theory of non smooth spaces with lower Ricci Curvature bounds has undergone huge developments in the last thirty years. On the one hand the impetus came from Gromov’s precompactness theorem
A. Mondino - Time-like Ricci curvature bounds via optimal transport
The goal of the talk is to present a recent work in collaboration with Cavalletti (SISSA) on optimal transport in Lorentzian synthetic spaces. The aim is to set up a “Lorentzian analog” of the
R. Bamler - Compactness and partial regularity theory of Ricci flows in higher dimensions
We present a new compactness theory of Ricci flows. This theory states that any sequence of Ricci flows that is pointed in an appropriate sense, subsequentially converges to a synthetic flow.
R. Perales - Recent Intrinsic Flat Convergence Theorems
Théorèmes récents de convergence plane intrinsèque
T. Ozuch - Noncollapsed degeneration and desingularization of Einstein 4-manifolds
We study the noncollapsed singularity formation of Einstein 4-manifolds. We prove that any smooth Einstein 4-manifold close to a singular one in a mere Gromov-Hausdorff (GH) sense is the result
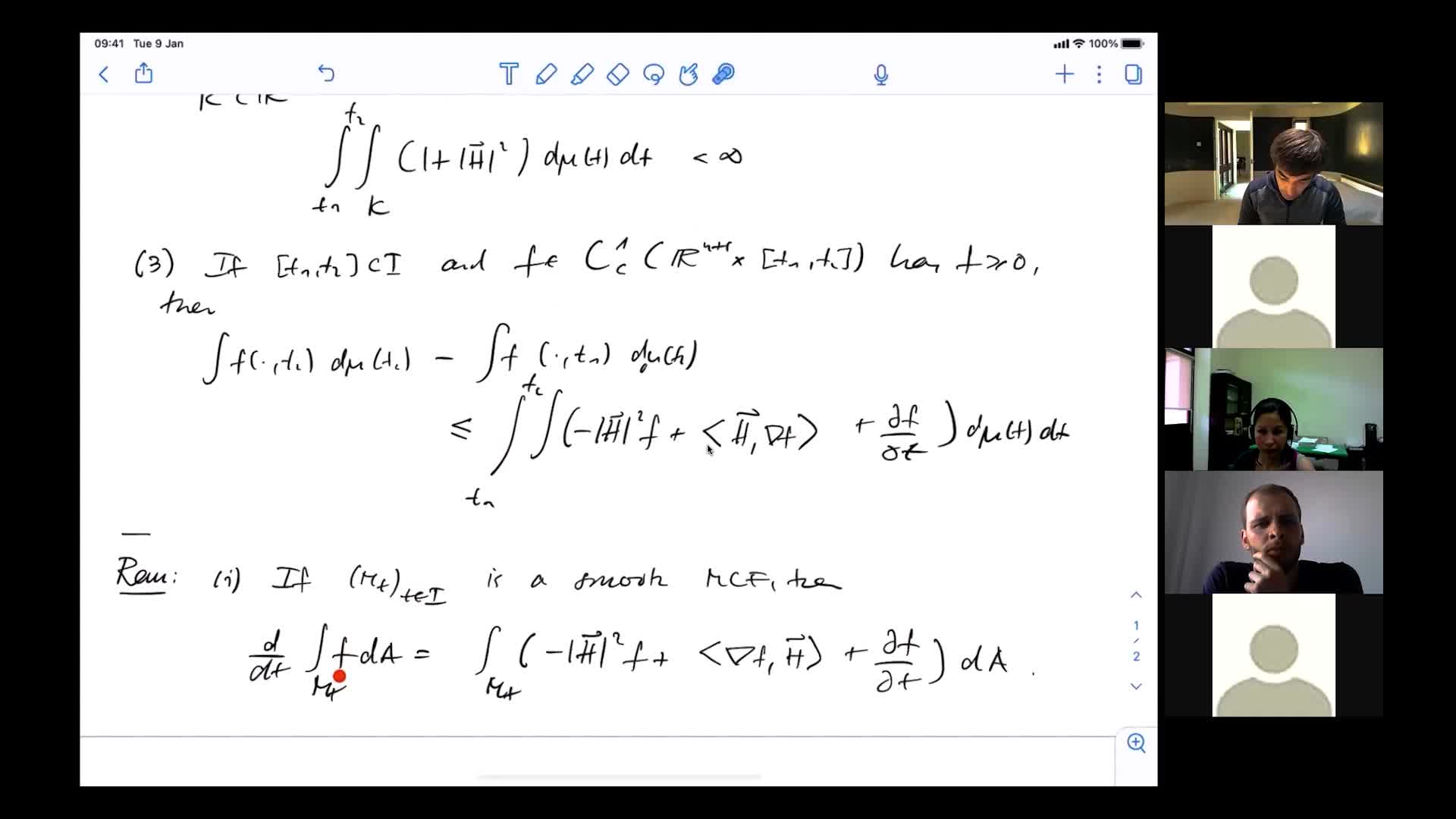
F. Schulze - Mean curvature flow with generic initial data
Mean curvature flow is the gradient flow of the area functional and constitutes a natural geometric heat equation on the space of hypersurfaces in an ambient Riemannian manifold. It is believed,
A. Song - On the essential minimal volume of Einstein 4-manifolds
Given a positive epsilon, a closed Einstein 4-manifold admits a natural thick-thin decomposition. I will explain how, for any delta, one can modify the Einstein metric to a bounded sectional
A. Lytchak - Convex subsets in generic manifolds
In the talk I would like to discuss some statements and questions about convex subsets and convex hulls in generic Riemannian manifolds of dimension at least 3. The statements, obtained jointly
C. Sormani - Intrinsic Flat and Gromov-Hausdorff Convergence 4
We introduce various notions of convergence of Riemannian manifolds and metric spaces. We then survey results and open questions concerning the limits of sequences of Riemannian manifolds with
C. Sormani - Intrinsic Flat and Gromov-Hausdorff Convergence 3
We introduce various notions of convergence of Riemannian manifolds and metric spaces. We then survey results and open questions concerning the limits of sequences of Riemannian manifolds with
C. Sormani - Intrinsic Flat and Gromov-Hausdorff Convergence 2
We introduce various notions of convergence of Riemannian manifolds and metric spaces. We then survey results and open questions concerning the limits of sequences of Riemannian manifolds with
C. Sormani - Intrinsic Flat and Gromov-Hausdorff Convergence 1
We introduce various notions of convergence of Riemannian manifolds and metric spaces. We then survey results and open questions concerning the limits of sequences of Riemannian manifolds with
A. Song - What is the (essential) minimal volume? 4
I will discuss the notion of minimal volume and some of its variants. The minimal volume of a manifold is defined as the infimum of the volume over all metrics with sectional curvature between
A. Song - What is the (essential) minimal volume? 3
I will discuss the notion of minimal volume and some of its variants. The minimal volume of a manifold is defined as the infimum of the volume over all metrics with sectional curvature between
A. Song - What is the (essential) minimal volume? 2
I will discuss the notion of minimal volume and some of its variants. The minimal volume of a manifold is defined as the infimum of the volume over all metrics with sectional curvature between
A. Song - What is the (essential) minimal volume? 1
I will discuss the notion of minimal volume and some of its variants. The minimal volume of a manifold is defined as the infimum of the volume over all metrics with sectional curvature between
F. Schulze - An introduction to weak mean curvature flow 4
It has become clear in recent years that to understand mean curvature flow through singularities it is essential to work with weak solutions to mean curvature flow. We will give a brief
F. Schulze - An introduction to weak mean curvature flow 3
It has become clear in recent years that to understand mean curvature flow through singularities it is essential to work with weak solutions to mean curvature flow. We will give a brief
F. Schulze - An introduction to weak mean curvature flow 2
It has become clear in recent years that to understand mean curvature flow through singularities it is essential to work with weak solutions to mean curvature flow. We will give a brief
F. Schulze - An introduction to weak mean curvature flow 1
It has become clear in recent years that to understand mean curvature flow through singularities it is essential to work with weak solutions to mean curvature flow. We will give a brief
T. Richard - Advanced basics of Riemannian geometry 4
We will present some of the tools used by the more advanced lectures. The topics discussed will include : Gromov Hausdorff distance, comparison theorems for sectional and Ricci curvature, the
T. Richard - Advanced basics of Riemannian geometry 3
We will present some of the tools used by the more advanced lectures. The topics discussed will include : Gromov Hausdorff distance, comparison theorems for sectional and Ricci curvature, the
T. Richard - Advanced basics of Riemannian geometry 2
We will present some of the tools used by the more advanced lectures. The topics discussed will include : Gromov Hausdorff distance, comparison theorems for sectional and Ricci curvature, the
T. Richard - Advanced basics of Riemannian geometry 1
We will present some of the tools used by the more advanced lectures. The topics discussed will include : Gromov Hausdorff distance, comparison theorems for sectional and Ricci curvature, the
A. Mondino - Metric measure spaces satisfying Ricci curvature lower bounds 4
The idea of compactifying the space of Riemannian manifolds satisfying Ricci curvature lower bounds goes back to Gromov in the '80ies and was pushed by Cheeger-Colding in the ‘90ies, who
A. Mondino - Metric measure spaces satisfying Ricci curvature lower bounds 3
The idea of compactifying the space of Riemannian manifolds satisfying Ricci curvature lower bounds goes back to Gromov in the '80ies and was pushed by Cheeger-Colding in the ‘90ies, who
A. Mondino - Metric measure spaces satisfying Ricci curvature lower bounds 2
The idea of compactifying the space of Riemannian manifolds satisfying Ricci curvature lower bounds goes back to Gromov in the '80ies and was pushed by Cheeger-Colding in the ‘90ies, who
A. Mondino - Metric measure spaces satisfying Ricci curvature lower bounds 1
The idea of compactifying the space of Riemannian manifolds satisfying Ricci curvature lower bounds goes back to Gromov in the '80ies and was pushed by Cheeger-Colding in the ‘90ies, who
G. Courtois - Compactness and Finiteness Results for Gromov-Hyperbolic Spaces 4
This is a series of lectures on Bishop--Gromov's type inequalities adapted to metric spaces. We consider the case of Gromov-hyperbolic spaces and draw consequences of these inequalities such as
G. Courtois - Compactness and Finiteness Results for Gromov-Hyperbolic Spaces 3
This is a series of lectures on Bishop--Gromov's type inequalities adapted to metric spaces. We consider the case of Gromov-hyperbolic spaces and draw consequences of these inequalities such as
G. Courtois - Compactness and Finiteness Results for Gromov-Hyperbolic Spaces 2
This is a series of lectures on Bishop--Gromov's type inequalities adapted to metric spaces. We consider the case of Gromov-hyperbolic spaces and draw consequences of these inequalities such as
G. Courtois - Compactness and Finiteness Results for Gromov-Hyperbolic Spaces 1
This is a series of lectures on Bishop--Gromov's type inequalities adapted to metric spaces. We consider the case of Gromov-hyperbolic spaces and draw consequences of these inequalities such as
P. Castillon - CAT(k)-spaces 4
The purpose of this course is to introduce the synthetic treatment of sectional curvature upper-bound on metric spaces. The basic idea of A.D. Alexandrov was to characterize the curvature bounds
P. Castillon - CAT(k)-spaces 3
The purpose of this course is to introduce the synthetic treatment of sectional curvature upper-bound on metric spaces. The basic idea of A.D. Alexandrov was to characterize the curvature bounds
P. Castillon - CAT(k)-spaces 2
The purpose of this course is to introduce the synthetic treatment of sectional curvature upper-bound on metric spaces. The basic idea of A.D. Alexandrov was to characterize the curvature bounds
G. Besson - CAT(k)-spaces 1
The purpose of this course is to introduce the synthetic treatment of sectional curvature upper-bound on metric spaces. The basic idea of A.D. Alexandrov was to characterize the curvature bounds
R. Bamler - Uniqueness of Weak Solutions to the Ricci Flow and Topological Applications 4
I will present recent work with Kleiner in which we verify two topological conjectures using Ricci flow. First, we classify the homotopy type of every 3-dimensional spherical space form. This
R. Bamler - Uniqueness of Weak Solutions to the Ricci Flow and Topological Applications 3
I will present recent work with Kleiner in which we verify two topological conjectures using Ricci flow. First, we classify the homotopy type of every 3-dimensional spherical space form. This
R. Bamler - Uniqueness of Weak Solutions to the Ricci Flow and Topological Applications 2
I will present recent work with Kleiner in which we verify two topological conjectures using Ricci flow. First, we classify the homotopy type of every 3-dimensional spherical space form. This
R. Bamler - Uniqueness of Weak Solutions to the Ricci Flow and Topological Applications 1
I will present recent work with Kleiner in which we verify two topological conjectures using Ricci flow. First, we classify the homotopy type of every 3-dimensional spherical space form. This
Intervenants et intervenantes
Professeur à l'Université de Berkeley (2021)
Mathématicien. Directeur de recherche au CNRS affecté au laboratoire de mathématiques pures de l'Institut Fourier (en 2001)
Mathématicienne. Titulaire d'un doctorat de l'Université de Californie Berkeley sous la direction de Richard Bamler. Spécialiste d'algèbre linéaire (2021)
Auteur d'une thèse de doctorat en mathématiques (Grenoble 1, 1997).
Maître de conférence à l'université de Montpellier et membre de l'Institut Montpelliérain Alexander Grothendieck (en 2022)
Mathématicien. Directeur de recherche CNRS, membre de l'équipe de recherche Analyse complexe et géométrie, Institut de mathématiques de Jussieu - Paris Rive gauche (IMJ-PRG, UMR 7586), Sorbonne université et Université de Paris (en 2021)
Docteur en mathématiques (Grenoble 1, 1987)
Membre du jury d'une thèse en Mathématiques à Université Côte d'Azur en 2025
Professeur, Université libre de Bruxelles, 2014
Codirecteur d'une thèse en Mathématiques à Aix-Marseille en 2022
Président du jury d'une thèse de doctorat en Mathématiques à Strasbourg en 2014
Titulaire d'un doctorat en arts plastiques à Paris 1 en 2009
Mathématicien. Post-doctorant en mathématiques à Harvard (2021)
Mathématicien. Mathematics Institute, University of Warwick, Coventry, UK (en 2019). Professeur de mathématiques, Mathematical Institute-University of Oxford (depuis 2019) (en 2021)
Mathématicien. Enseignant au Massachusetts Institute of Technology (MIT) depuis 2020.
Docteure en mathématiques de la Stony Brook University depuis 2015. En poste à l'Institut de mathématiques de l'Université Nationale Autonome du mexique (Oaxaca) (2021)
Auteur d'une thèse en mathématiques à Grenoble en 2012
Professeur de l'Institut mathématiques à l'université de Warwick dans le groupe d'analyse géométrique (2021)
Mathématicien. Chercheur au Mathematical Institute de l'Université d'Oxford (2021)
Mathématicien actif en France et en Californie
Professeure au département de mathématiques au Lehman College (City University of New York) (2021)
Auteur d'une Thèse de 3e cycle en Statistique mathématique. Analyse des données à Paris 6 en 1984
Titulaire d'un doctorat en mathématiques fondamentales de l'université Paris sciences et lettres (2018)
Ecrit aussi en anglais Enseigne à la School of Mathematics and Computer Science, Fujian Normal University, Fuzhou, Chine (en 2013)