Notice
3.10. Decoding One Out of Many
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
The final session of this week isdevoted to Decoding One Out of Many. Decoding One Out of Manyis interested in solving the following variantof Syndrome Decoding. In this variant, the onlydifference with the usual Syndrome Decoding isthat we are interested in a set of syndromesrather than a single syndrome. So, the instance will be S, a set of syndromes of size N. H, a parity-checkmatrix and w an integer, the weight we are looking for. And we are interestedin an error e, such that the syndrome of e is anelement of the set S with e of weight w or less. We will denote CSD sub N of H, S, w, the set of allsolutions to the above problem. As for CSD1 which is, infact, the plain CSD, we will only consider solvable instances. And by solvable hereinstances, we mean something very strong, we meanthat every syndrome in the set S belongs to that set. So, every syndrome inthe set S corresponds to an error of weight w. We expect with thistechnique - and I will show you how we obtain this -, weexpect to get all solutions, the N solution to the problem atthe expense of a factor only √ N. Or alternatively, weexpect to get a single solution to the problem,but to gain a factor √ N to obtain that solution. Again, I will startwith Birthday Decoding. Now, I want to solveBirthday Decoding with multiple instances. I will now split the matrix intotwo parts, but you can see here that n1 will be larger than n2, that is the left partof the matrix is larger than the right part of the matrix. Also, the weight w,instead of being divided in two equal parts is divided in w1+w2, and possibly one of thoseweights, in fact, it will be w1, is greater thanthe other part w2. I define those two sets:the first set is simply a set of syndromes of errorse1*(H1 transpose) when the weight of e1 is w1. But the second listis in fact formed of the syndrome according to H2that is e2*(H2 transpose) + any syndrome s. So, the list L2 will
have a size equal to the number of syndromes N * (n2, w2)that is the number of errors of weight w2, when the first list L1 will have simply a size (n1,w1).
Intervention / Responsable scientifique
Dans la même collection
-
3.6. Stern/Dumer Algorithm
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we will present the Stern algorithm for decoding. In fact, the idea is to combine two algorithms that we have seen before, the Lee and Brickell algorithm and the Birthday Decoding.
-
3.1. From Generic Decoding to Syndrome Decoding
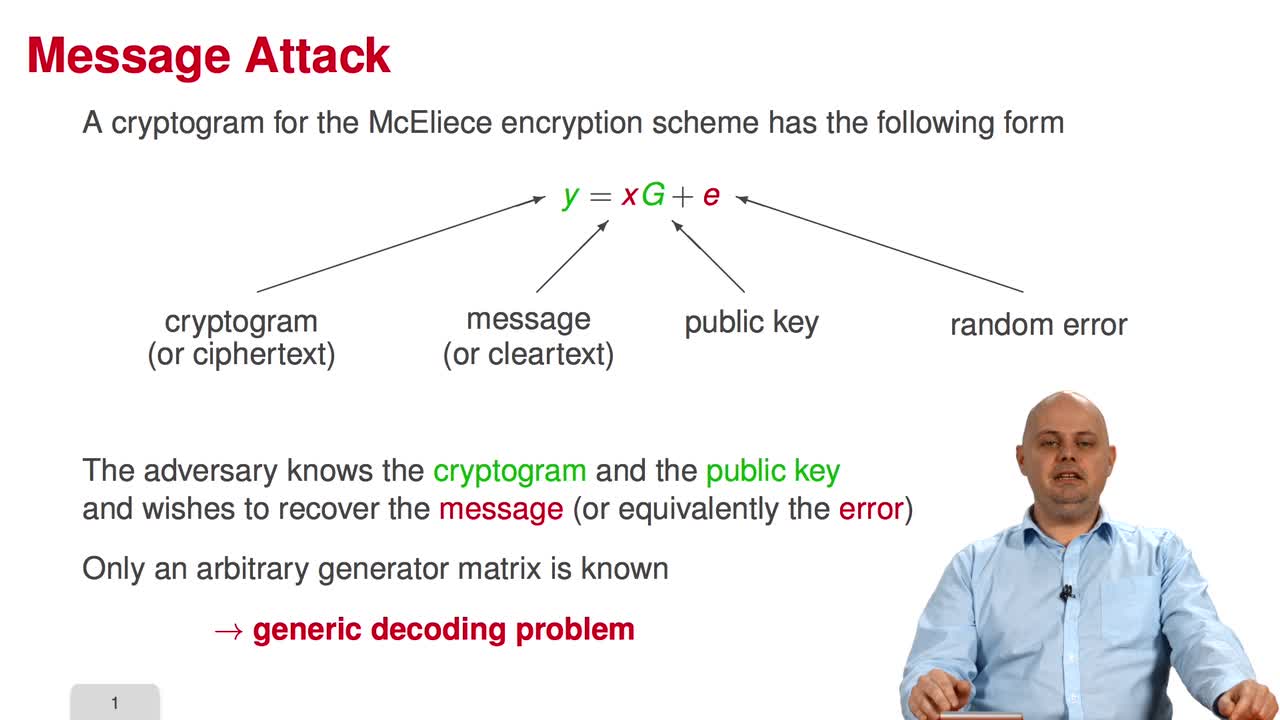
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuWelcome to the third week of the MOOC on code-based cryptography. This week, we will learn about message attacks. Among the ten sessions of this week, the first six will present the most essential
-
3.9. Generalized Birthday Algorithm for Decoding
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuThe session nine is devoted to the application of the Generalized Birthday Algorithm to decoding. The Generalized Birthday Algorithm was presented by David Wagner in 2002, in a more general
-
3.4. Complexity Analysis
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, I will present the main technique to make the analysis of the various algorithms presented in this course. So, Information Set Decoding refers to a family of algorithms which is
-
3.7. May, Meurer, and Thomae Algorithm
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuSo, with the session 7 we are entering the most advanced part of that course. The idea of what I called the Improved Birthday Decoding is to use the so-called "representation technique" introduced
-
3.2. Combinatorial Solutions: Exhaustive Search and Birthday Decoding
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, I will detail two combinatorial solutions to the decoding problem. The first one is the Exhaustive Search. To find our w columns, we will simply enumerate all the tuples j1 to jw
-
3.5. Lee and Brickell Algorithm
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this fifth session, we will study a variant of information set decoding proposed by Lee and Brickell. So, the main idea consists in relaxing the Prange algorithm to amortize the cost of the
-
3.8. Becker, Joux, May, and Meurer Algorithm
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuNow in session 8, we will present yet another evolution of information set decoding. Before presenting this improvement, we will first improve the Birthday Decoding algorithm what I call a Further
-
3.3. Information Set Decoding: the Power of Linear Algebra
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this third session, we will present the most important concept of the week: Information Set Decoding. The problem of decoding is not only a combinatorial problem. Because we are dealing with
Avec les mêmes intervenants et intervenantes
-
5.2. The Courtois-Finiasz-Sendrier (CFS) Construction
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, I am going to present the Courtois-Finiasz-Sendrier Construction of a code-based digital signature. In the previous session, we have seen that it is impossible to hash a document
-
4.6. Attack against GRS codes
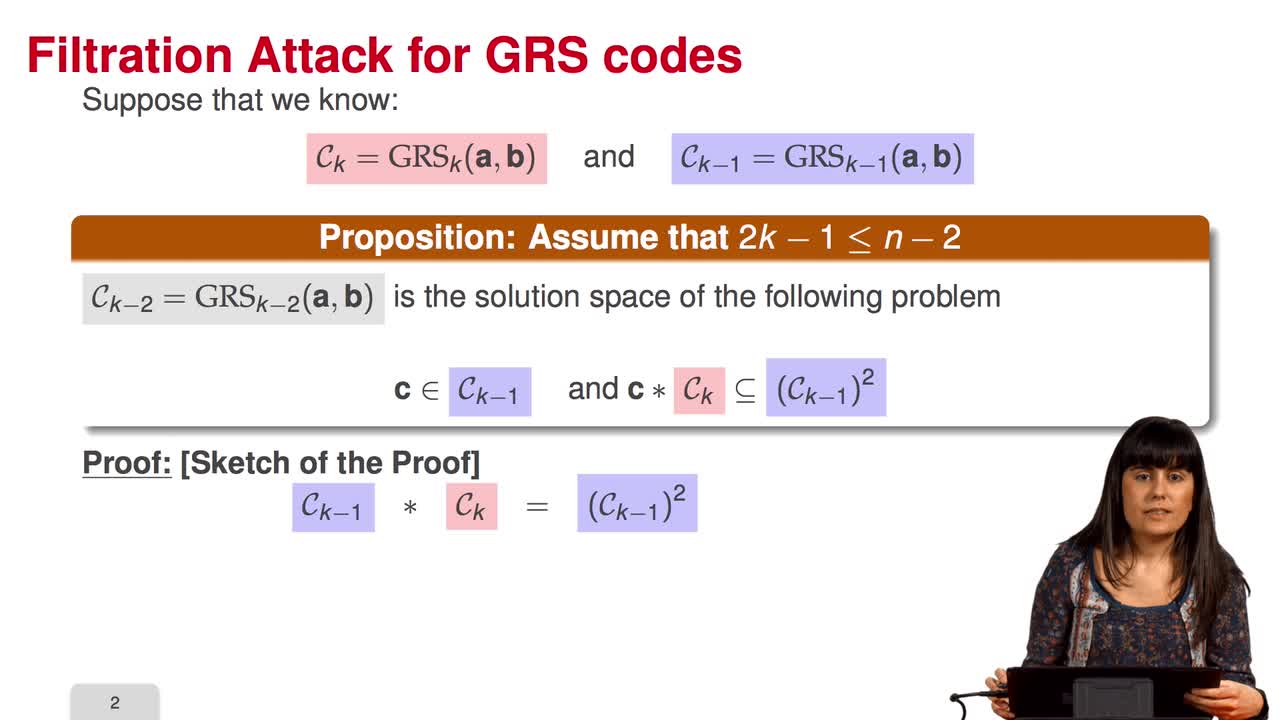
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session we will discuss the proposal of using generalized Reed-Solomon codes for the McEliece cryptosystem. As we have already said, generalized Reed-Solomon codes were proposed in 1986 by
-
5.5. Stern’s Zero-Knowledge Identification Scheme
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we are going to have a look at Stern’s Zero-Knowledge Identification Scheme. So, what is a Zero-Knowledge Identification Scheme? An identification scheme allows a prover to prove
-
4.9. Goppa codes still resist
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuAll the results that we have seen this week doesn't mean that code based cryptography is broken. So in this session we will see that Goppa code still resists to all these attacks. So recall that
-
4.4. Attack against subcodes of GRS codes
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we will talk about using subcodes of a Generalized Reed–Solomon code for the McEliece Cryptosystem. Recall that to avoid the attack of Sidelnikov and Shestakov, Berger and
-
5.3. Attacks against the CFS Scheme
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we will have a look at the attacks against the CFS signature scheme. As for public-key encryption, there are two kinds of attacks against signature schemes. First kind of attack is
-
4.7. Attack against Reed-Muller codes
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we will introduce an attack against binary Reed-Muller codes. Reed-Muller codes were introduced by Muller in 1954 and, later, Reed provided the first efficient decoding algorithm
-
5.6. An Efficient Provably Secure One-Way Function
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we are going to see how to build an efficient provably secure one-way function from coding theory. As you know, a one-way function is a function which is simple to evaluate and
-
5.1. Code-Based Digital Signatures
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuWelcome to the last week of this MOOC on code-based cryptography. This week, we will be discussing other cryptographic constructions relying on coding theory. We have seen how to do public key
-
4.5. Error-Correcting Pairs
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuWe present in this session a general decoding method for linear codes. And we will see it in an example. Let C be a generalized Reed-Solomon code of dimension k associated to the pair (c, d). Then,
-
5.4. Parallel-CFS
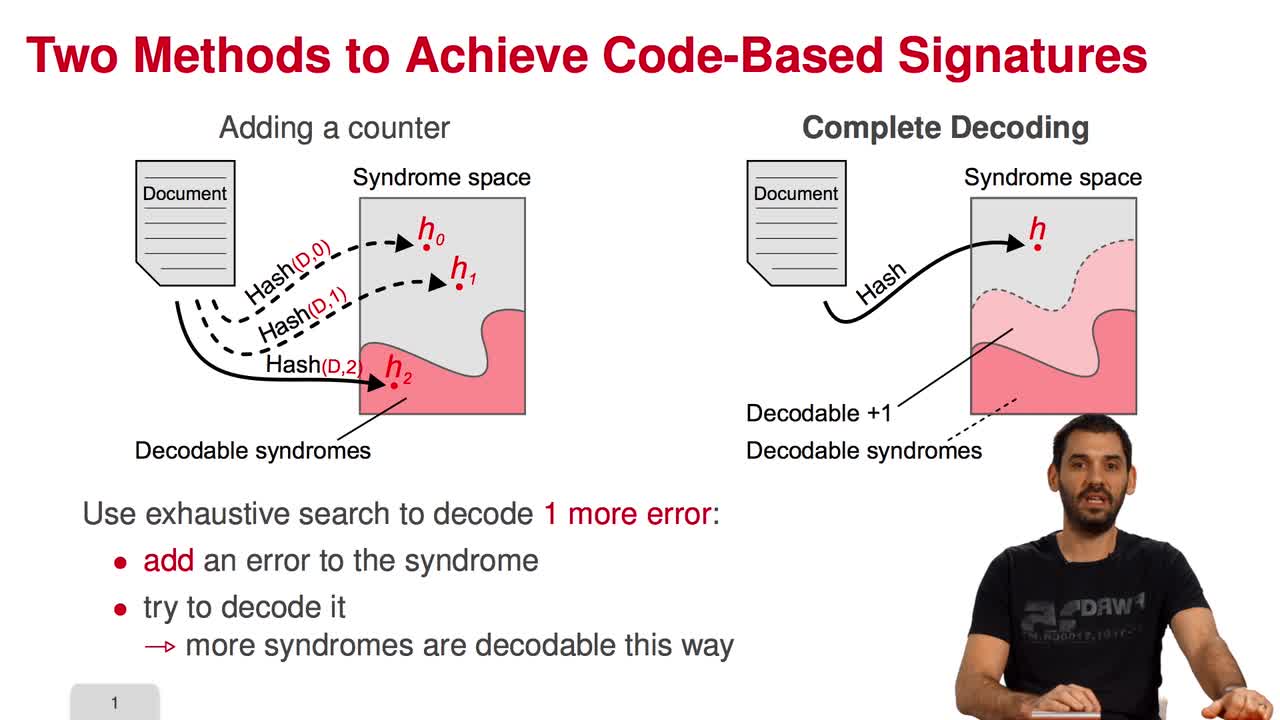
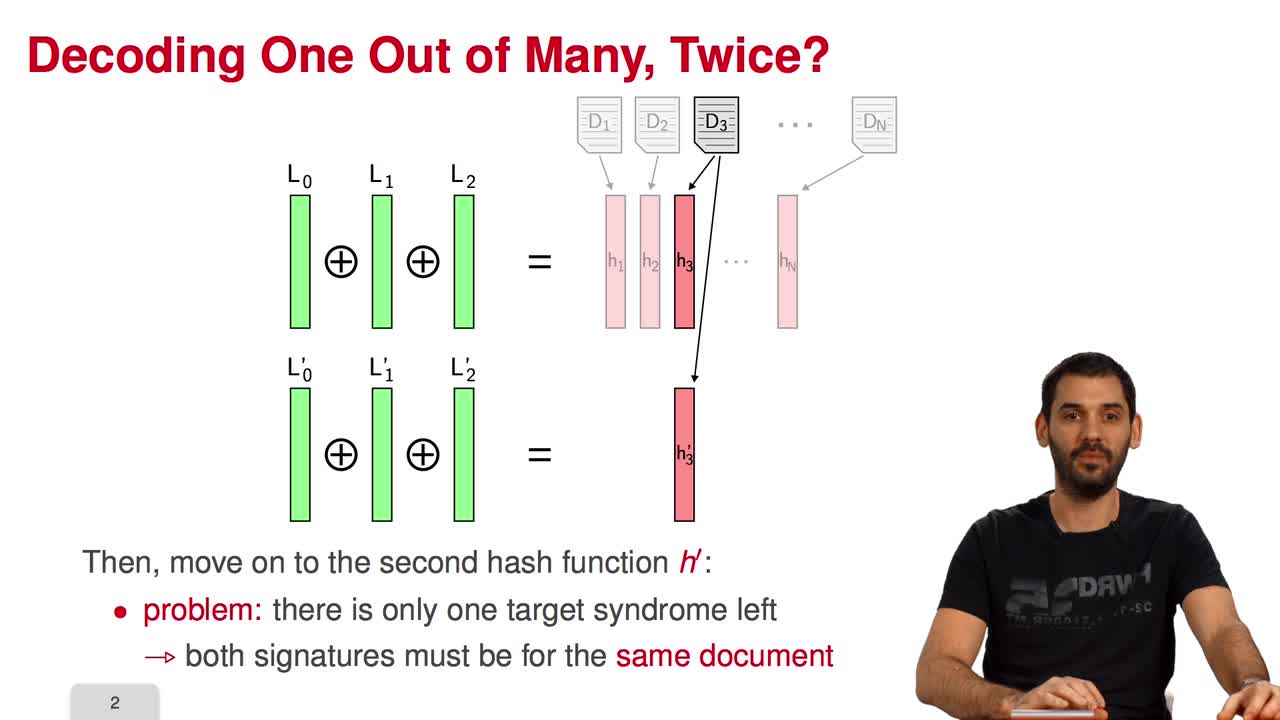
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, I will present a variant of the CFS signature scheme called parallel-CFS. We start from a simple question: what happens if you try to use two different hash functions and compute
-
4.8. Attack against Algebraic Geometry codes
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we will present an attack against Algebraic Geometry codes (AG codes). Algebraic Geometry codes is determined by a triple. First of all, an algebraic curve of genus g, then a n
Sur le même thème
-
La voix, une donnée identifiante à protéger
VincentEmmanuelEmmanuel Vincent, chercheur au Centre Inria de l'Université de Lorraine et au Loria (Laboratoire lorrain de recherche en informatique et ses applications), présente sa recherche sur l'anonymisation de
-
Podcast 1/4 d'heure avec : Emmanuel Vincent, chercheur au Centre Inria de l'Université de Lorraine …
VincentEmmanuelRencontre avec Emmanuel Vincent - chercheur au Centre Inria de l'Université de Lorraine et Loria (Laboratoire lorrain de recherche en informatique et ses applications).
-
Tuan Ta Pesao : écritures de sable et de ficelle à l'Ile d'Ambrym
VandendriesscheEricCe film se déroule au Nord de l’île d’Ambrym, dans l’archipel de Vanuatu, en Mélanésie...
-
Machines algorithmiques, mythes et réalités
MazenodVincentVincent Mazenod, informaticien, partage le fruit de ses réflexions sur l'évolution des outils numériques, en lien avec les problématiques de souveraineté, de sécurité et de vie privée...
-
Désassemblons le numérique - #Episode11 : Les algorithmes façonnent-ils notre société ?
SchwartzArnaudLima PillaLaércioEstériePierreSalletFrédéricFerbosAudeRoumanosRayyaChraibi KadoudIkramUn an après le tout premier hackathon sur les méthodologies d'enquêtes journalistiques sur les algorithmes, ce nouvel épisode part à la rencontre de différents points de vue sur les algorithmes.
-
Les machines à enseigner. Du livre à l'IA...
BruillardÉricQue peut-on, que doit-on déléguer à des machines ? C'est l'une des questions explorées par Éric Bruillard qui, du livre aux IA génératives, expose l'évolution des machines à enseigner...
-
Quel est le prix à payer pour la sécurité de nos données ?
MinaudBriceÀ l'ère du tout connecté, la question de la sécurité de nos données personnelles est devenue primordiale. Comment faire pour garder le contrôle de nos données ? Comment déjouer les pièges de plus en
-
Désassemblons le numérique - #Episode9 : Bientôt des supercalculateurs dans nos piscines ?
BeaumontOlivierBouzelRémiDes supercalculateurs feraient-ils bientôt leur apparition dans les piscines municipales pour les chauffer ? Réponses d'Olivier Beaumont, responsable de l'équipe-projet Topal, et Rémi Bouzel,
-
Des systèmes de numération pour le calcul modulaire
BajardJean-ClaudeLe calcul modulaire est utilisé dans de nombreuses applications des mathématiques...
-
Projection methods for community detection in complex networks
LitvakNellyCommunity detection is one of most prominent tasks in the analysis of complex networks such as social networks, biological networks, and the world wide web. A community is loosely defined as a group
-
Lara Croft. doing fieldwork under surveillance
Dall'AgnolaJasminLara Croft. Doing Fieldwork Under Surveillance Intervention de Jasmin Dall'Agnola (The George Washington University), dans le cadre du Colloque coorganisé par Anders Albrechtslund, professeur en
-
Containing predictive tokens in the EU
CzarnockiJanContaining Predictive Tokens in the EU – Mapping the Laws Against Digital Surveillance, intervention de Jan Czarnocki (KU Leuven), dans le cadre du Colloque coorganisé par Anders Albrechtslund,