Notice
5.2. The Courtois-Finiasz-Sendrier (CFS) Construction
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
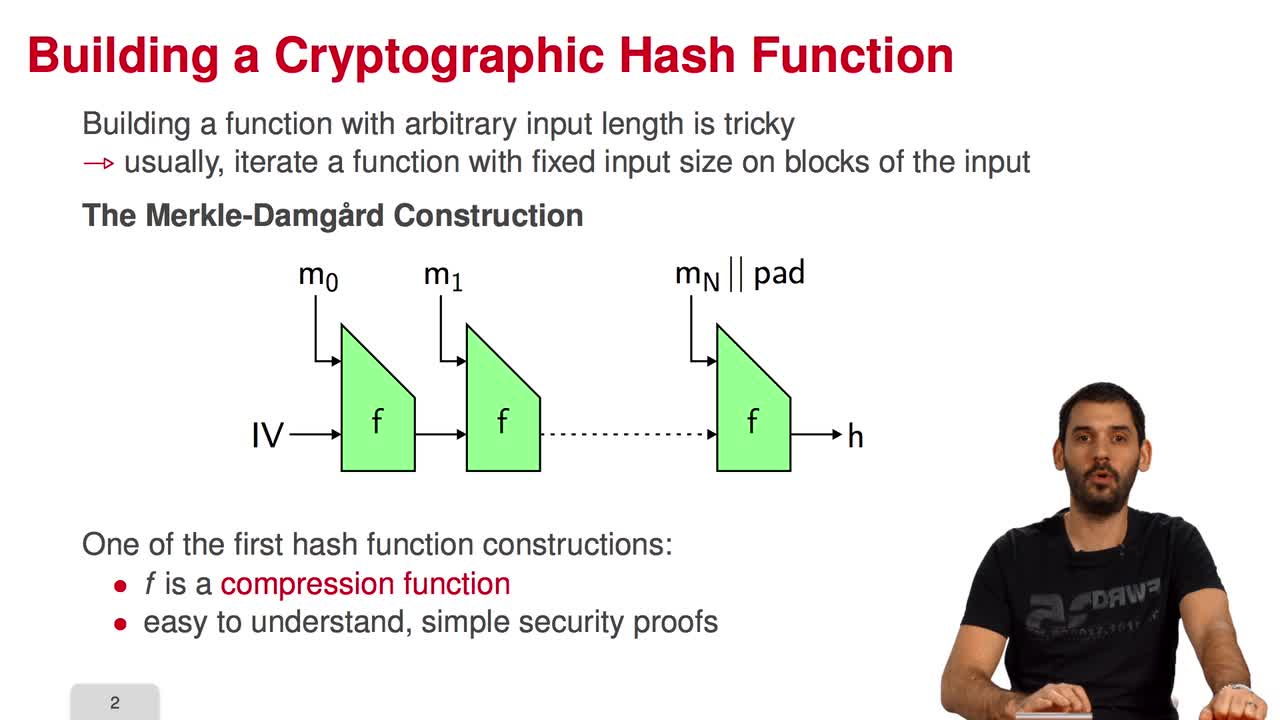
In this session, I amgoing to present the Courtois-Finiasz-SendrierConstruction of a code-based digital signature. In the previous session,we have seen that it is impossible to hash adocument into decodable syndromes. But it is possible to hashonto the space of all syndromes. The document is not always decodable. And we are going to see twotechniques to work around this problem. The first technique is toadd a counter to the document. This way, we hash both thecounter and the document and obtain a hash which is tied toboth the document and the counter. We increment the counter untila decodable syndrome is found. The signature is thedecoding of the syndrome but also contains the counter which isrequired for the verification. The second method is toperform complete decoding. Complete decoding is theidea of being able to decode any syndrome in the space. Andfor this, we need to modify the decoding algorithm.The idea is to add some exhaustive search tothe decoding algorithm. For example, if we want todecode one more error in the decoding capacity of thecode, we simply do an exhaustive search on one position. Add this errorto the syndrome and try to decode it. We can do the same with twoerrors or up to δ errors by doing a search on δ positions. This way, we can reach thecovering radius, which is the number of errors we need tocorrect to decode any element in the syndrome space. Both techniques are expensive. Decodable syndromes musthave high enough density in the space of all syndromes. Thecovering radius and decoding capacity must beclose to one another. If they are too distant,it will be too expensive to perform complete decoding. What are the requirements forcode-based digital signatures? As for a public-keyencryption, we need to be able to keep the decoding algorithm secret. So, we need codes where it ispossible to hide the structure efficiently. Binary Goppa codes areone of very few candidates. And so, we will use thisin the construction, exactly like in the original McEliece scheme. Then, to have someefficient signature schemes, we need the highest possibledensity of decodable syndromes.
Intervention
Dans la même collection
-
5.3. Attacks against the CFS Scheme
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we will have a look at the attacks against the CFS signature scheme. As for public-key encryption, there are two kinds of attacks against signature schemes. First kind of attack is
-
5.6. An Efficient Provably Secure One-Way Function
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we are going to see how to build an efficient provably secure one-way function from coding theory. As you know, a one-way function is a function which is simple to evaluate and
-
5.4. Parallel-CFS
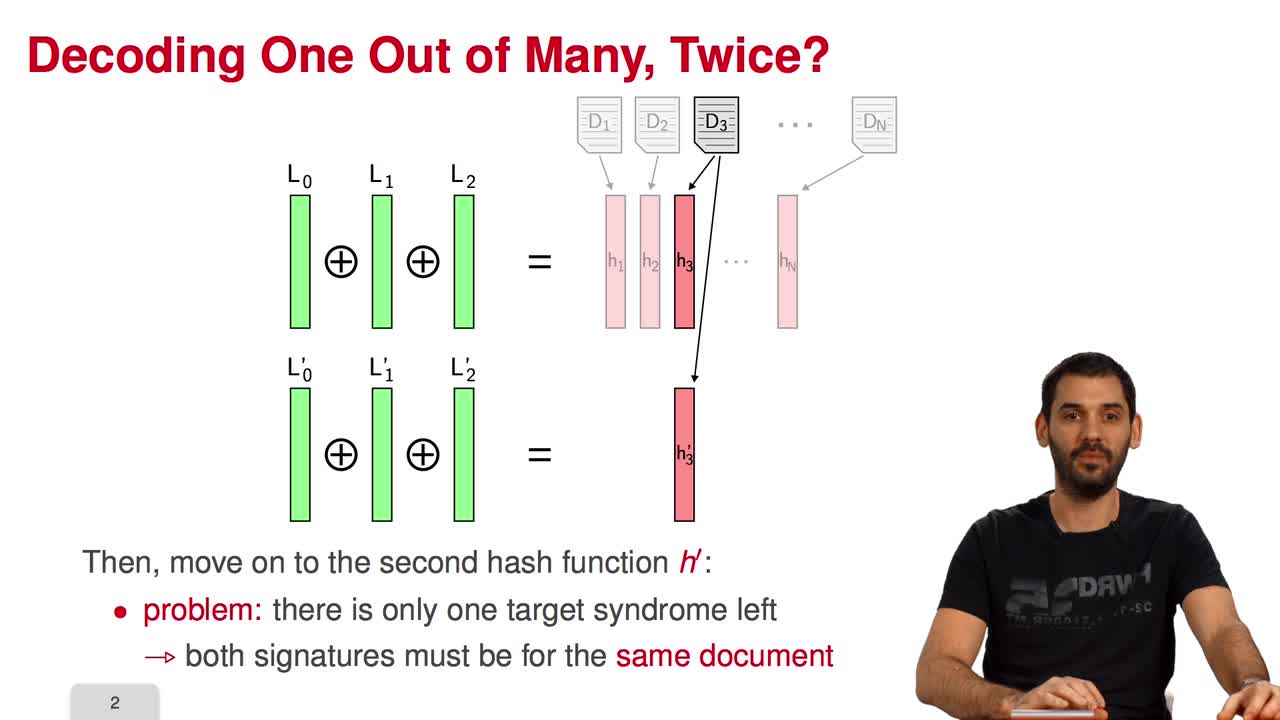
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, I will present a variant of the CFS signature scheme called parallel-CFS. We start from a simple question: what happens if you try to use two different hash functions and compute
-
5.7. The Fast Syndrome-Based (FSB) Hash Function
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn the last session of this week, we will have a look at the FSB Hash Function which is built using the one-way function we saw in the previous session. What are the requirements for a
-
5.1. Code-Based Digital Signatures
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuWelcome to the last week of this MOOC on code-based cryptography. This week, we will be discussing other cryptographic constructions relying on coding theory. We have seen how to do public key
-
5.5. Stern’s Zero-Knowledge Identification Scheme
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we are going to have a look at Stern’s Zero-Knowledge Identification Scheme. So, what is a Zero-Knowledge Identification Scheme? An identification scheme allows a prover to prove
Avec les mêmes intervenants et intervenantes
-
4.6. Attack against GRS codes
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session we will discuss the proposal of using generalized Reed-Solomon codes for the McEliece cryptosystem. As we have already said, generalized Reed-Solomon codes were proposed in 1986 by
-
5.6. An Efficient Provably Secure One-Way Function
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we are going to see how to build an efficient provably secure one-way function from coding theory. As you know, a one-way function is a function which is simple to evaluate and
-
4.9. Goppa codes still resist
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuAll the results that we have seen this week doesn't mean that code based cryptography is broken. So in this session we will see that Goppa code still resists to all these attacks. So recall that
-
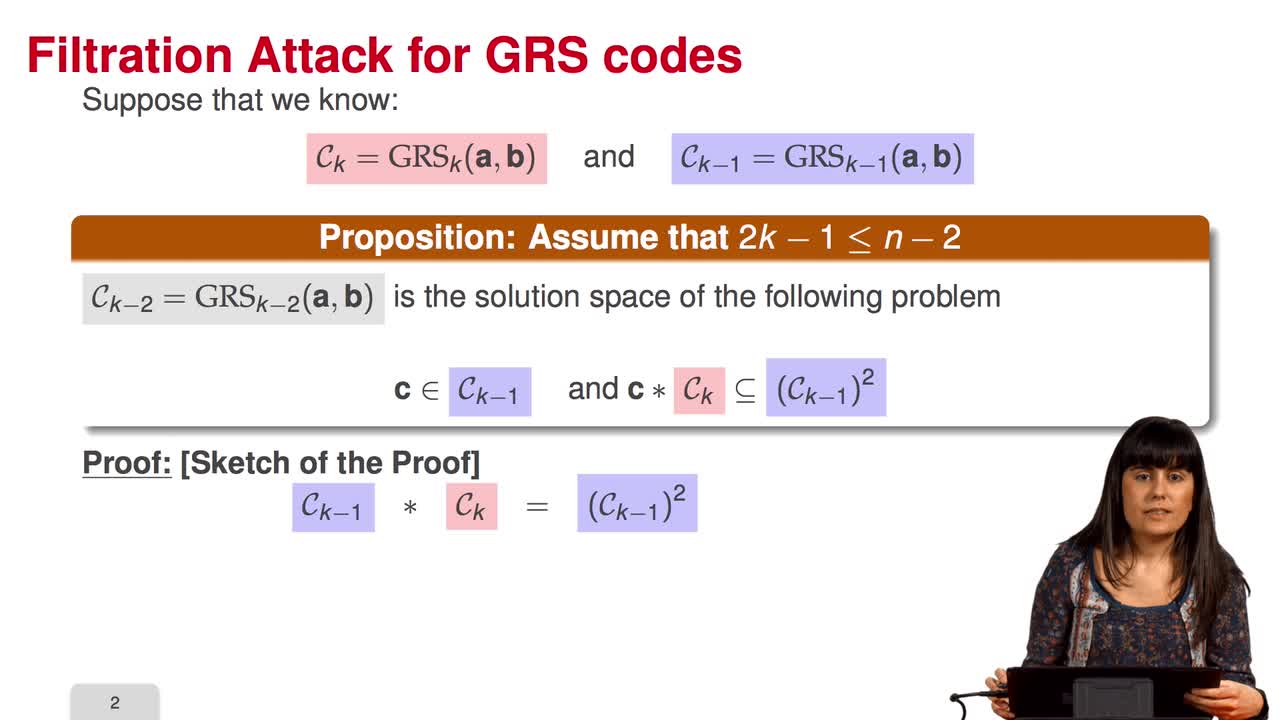
4.4. Attack against subcodes of GRS codes
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we will talk about using subcodes of a Generalized Reed–Solomon code for the McEliece Cryptosystem. Recall that to avoid the attack of Sidelnikov and Shestakov, Berger and
-
5.4. Parallel-CFS
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, I will present a variant of the CFS signature scheme called parallel-CFS. We start from a simple question: what happens if you try to use two different hash functions and compute
-
4.7. Attack against Reed-Muller codes
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we will introduce an attack against binary Reed-Muller codes. Reed-Muller codes were introduced by Muller in 1954 and, later, Reed provided the first efficient decoding algorithm
-
5.7. The Fast Syndrome-Based (FSB) Hash Function
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn the last session of this week, we will have a look at the FSB Hash Function which is built using the one-way function we saw in the previous session. What are the requirements for a
-
5.1. Code-Based Digital Signatures
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuWelcome to the last week of this MOOC on code-based cryptography. This week, we will be discussing other cryptographic constructions relying on coding theory. We have seen how to do public key
-
4.5. Error-Correcting Pairs
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuWe present in this session a general decoding method for linear codes. And we will see it in an example. Let C be a generalized Reed-Solomon code of dimension k associated to the pair (c, d). Then,
-
5.5. Stern’s Zero-Knowledge Identification Scheme
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we are going to have a look at Stern’s Zero-Knowledge Identification Scheme. So, what is a Zero-Knowledge Identification Scheme? An identification scheme allows a prover to prove
-
4.8. Attack against Algebraic Geometry codes
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we will present an attack against Algebraic Geometry codes (AG codes). Algebraic Geometry codes is determined by a triple. First of all, an algebraic curve of genus g, then a n
-
5.3. Attacks against the CFS Scheme
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we will have a look at the attacks against the CFS signature scheme. As for public-key encryption, there are two kinds of attacks against signature schemes. First kind of attack is
Sur le même thème
-
Projection methods for community detection in complex networks
LitvakNellyCommunity detection is one of most prominent tasks in the analysis of complex networks such as social networks, biological networks, and the world wide web. A community is loosely defined as a group
-
Lara Croft. doing fieldwork under surveillance
Dall'AgnolaJasminLara Croft. Doing Fieldwork Under Surveillance Intervention de Jasmin Dall'Agnola (The George Washington University), dans le cadre du Colloque coorganisé par Anders Albrechtslund, professeur en
-
Containing predictive tokens in the EU
CzarnockiJanContaining Predictive Tokens in the EU – Mapping the Laws Against Digital Surveillance, intervention de Jan Czarnocki (KU Leuven), dans le cadre du Colloque coorganisé par Anders Albrechtslund,
-
Inauguration de l'exposition - Vanessa Vitse : Nombres de Sophie Germain et codes secrets
VitseVanessaExposé de Vanessa Vitse (Institut Fourier) : Nombres de Sophie Germain et codes secrets
-
"Le mathématicien Petre (Pierre) Sergescu, historien des sciences, personnalité du XXe siècle"
HerléaAlexandreAlexandre HERLEA est membre de la section « Sciences, histoire des sciences et des techniques et archéologie industrielle » du CTHS. Professeur émérite des universités, membre effectif de l'Académie
-
Ivan Murit - Processus de création d'images
MuritIvanJe vais présenter une manière décalée d'aborder les outils d'impression. Pour cela nous ne partirons pas de l'envie d'imprimer une image préexistante, mais d'avant cela : comment se crée une forme
-
Retour d'expérience sur l'utilisation croisée de plusieurs archives de fouilles
TufféryChristopheDans le cadre d'une thèse de doctorat engagée depuis 2019, une étude historiographique et épistémologique des effets des dispositifs numériques sur l'archéologie et sur les archéologues au cours des
-
Information Structures for Privacy and Fairness
PalamidessiCatusciaInformation Structures for Privacy and Fairness
-
Le Creativ’Lab, au cœur de la robotique et de l’intelligence artificielle (ASR N°18 - LORIA)
HénaffPatrickLefebvreSylvainLe LORIA, laboratoire phare de la Grande Région dans le domaine de l’informatique, propose de rendre la recherche plus ouverte, plus collaborative, plus ambitieuse… en un mot, plus créative, à travers
-
AI and Human Decision-Making: An Interdisciplinary Perspective
CastellucciaClaudeThis seminar will talk about some of the privacy risks of these systems and will describe some recent attacks. It will also discuss why they sometimes fail to deliver. Finally, we will also show that
-
Webinaire sur la rédaction des PGD
LouvetViolaineRédaction des Plans de Gestion de Données (PGD) sous l’angle des besoins de la communauté mathématique.
-
Les algorithmes de Parcoursup
MathieuClaireL’objectif de la journée « Algorithmes d’aide à la décision publique » était de sensibiliser le grand public aux rôles des algorithmes d’aide à la décision publique utilisés par exemple pour l
