Notice
Alexander Strohmaier - Workshop
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
I will explain how one can formulate and formalize the Gupta Bleuler framework for the Quantization of the electromagnetic field in an algebraic manner so that it works on globally hyperbolic space times. I will then discuss a construction of physical representations that works without the "spectral gap assumption" in the case of absense of zero energy resonances. These can be excluded by topologocial restrictions at infinity. This is based on joint work with Felix Finster.
Documentation
Liens
Dans la même collection
-
Lionel Mason - Perturbative formulae for scattering of gravitational wave
MasonLionel J.The Christodoulou Klainerman proof of existence of asymptotically simple space-times shows that it is reasonable to consider the scattering of
-
Andras Vasy - Microlocal analysis and wave propagation (Part 4)
In these lectures I will explain the basics of microlocal analysis, emphasizing non elliptic problems, such as wave propagation, both on manifolds without boundary, and on manifolds with boundary. In
-
-
Andras Vasy - Microlocal analysis and wave propagation (Part 1)
VasyAndrásIn these lectures I will explain the basics of microlocal analysis, emphasizing non elliptic problems, such as wave propagation, both on
-
-
Alain Bachelot - Waves in the Anti-de Sitter space-time Ads
BachelotAlainIn this talk we address some issues concerning the wave propagation in the 4D+1 anti de Sitter space time : the role of the conformal
-
Semyon Dyatlov - Spectral gaps for normally hyperbolic trapping
DyatlovSemyonMotivated by wave decay for Kerr and Kerr de Sitter black holes, we study spectral gaps for codimension 2 normally hyperbolic trapped sets with
-
Andras Vasy - Microlocal analysis and wave propagation (Part 3)
In these lectures I will explain the basics of microlocal analysis, emphasizing non elliptic problems, such as wave propagation, both on manifolds without boundary, and on manifolds with boundary. In
-
Maciej Zworski - From redshift effect to classical dynamics : microlocal proof of Smale's conjecture
ZworskiMaciejDynamical zeta functions of Selberg, Smale and Ruelle are analogous to the Riemann zeta function with the product over primes replaced by
-
Pieter Blue - Decay for fields outside black holes
BluePieterI will discuss energy and Morawetz (or integrated local decay) estimates for fields outside black holes. These results build on results for
-
Jérémie Szeftel - General relativity (Workshop)
SzeftelJérémieIn order to control locally a space time which satisfies the Einstein equations, what are the minimal assumptions one should make on its
-
Philippe G LeFloch - Weakly regular spacetimes with T2 symmetry
LeFlochPhilippe G.I will discuss the initial value problem for the Einstein equations and present results concerning the existence and asymptotic behavior of
Sur le même thème
-
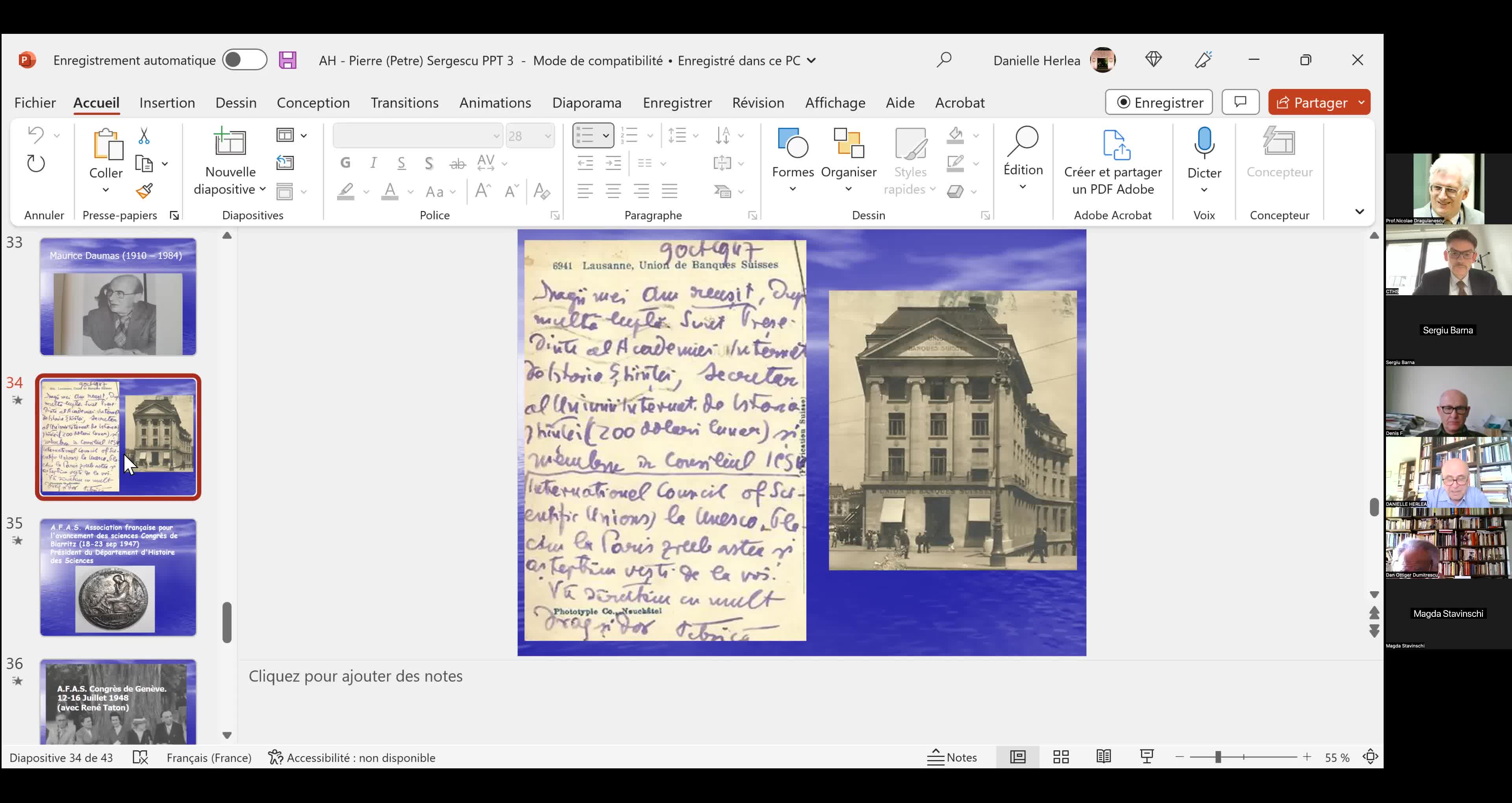
"Le mathématicien Petre (Pierre) Sergescu, historien des sciences, personnalité du XXe siècle"
HerléaAlexandreAlexandre HERLEA est membre de la section « Sciences, histoire des sciences et des techniques et archéologie industrielle » du CTHS. Professeur émérite des universités, membre effectif de l'Académie
-
Webinaire sur la rédaction des PGD
LouvetViolaineRédaction des Plans de Gestion de Données (PGD) sous l’angle des besoins de la communauté mathématique.
-
Alexandre Booms : « Usage de matériel pédagogique adapté en géométrie : une transposition à interro…
« Usage de matériel pédagogique adapté en géométrie : une transposition à interroger ». Alexandre Booms, doctorant (Université de Reims Champagne-Ardenne - Cérep UR 4692)
-
R. Bamler - Compactness and partial regularity theory of Ricci flows in higher dimensions
BamlerRichard H.We present a new compactness theory of Ricci flows. This theory states that any sequence of Ricci flows that is pointed in an appropriate sense, subsequentially converges to a synthetic flow.
-
P. Burkhardt - Pointwise lower scalar curvature bounds for C0 metrics via regularizing Ricci flow
Burkhardt-GuimPaulaWe propose a class of local definitions of weak lower scalar curvature bounds that is well defined for C0 metrics. We show the following: that our definitions are stable under greater-than-second
-
C. Li - Classifying sufficiently connected PSC manifolds in 4 and 5 dimensions
LiChaoIn this talk, I will discuss some recent developments on the topology of closed manifolds admitting Riemannian metrics of positive scalar curvature. In particular, we will prove if a closed PSC
-
T. Ozuch - Noncollapsed degeneration and desingularization of Einstein 4-manifolds
OzuchTristanWe study the noncollapsed singularity formation of Einstein 4-manifolds. We prove that any smooth Einstein 4-manifold close to a singular one in a mere Gromov-Hausdorff (GH) sense is the result
-
D. Tewodrose - Limits of Riemannian manifolds satisfying a uniform Kato condition
TewodroseDavidPresentation of a joint work with G. Carron and I. Mondello where we study Kato limit spaces.
-
Y. Lai - A family of 3d steady gradient Ricci solitons that are flying wings
LaiYiWe find a family of 3d steady gradient Ricci solitons that are flying wings. This verifies a conjecture by Hamilton. For a 3d flying wing, we show that the scalar curvature does not vanish at
-
A. Mondino - Time-like Ricci curvature bounds via optimal transport
MondinoAndreaThe goal of the talk is to present a recent work in collaboration with Cavalletti (SISSA) on optimal transport in Lorentzian synthetic spaces. The aim is to set up a “Lorentzian analog” of the
-
M. Lesourd - Positive Scalar Curvature on Noncompact Manifolds and the Positive Mass Theorem
LesourdMartinThe study of positive scalar curvature on noncompact manifolds has seen significant progress in the last few years. A major role has been played by Gromov's results and conjectures, and in
-
R. Perales - Recent Intrinsic Flat Convergence Theorems
PeralesRaquelThéorèmes récents de convergence plane intrinsèque
