Notice
3.9. Generalized Birthday Algorithm for Decoding
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
The session nine isdevoted to the application of the Generalized BirthdayAlgorithm to decoding. The Generalized BirthdayAlgorithm was presented by David Wagner in 2002, in amore general context. In fact, at order a,the Generalized Birthday Algorithm solves thefollowing problem: we are given 2^a lists of vectors of size L and we want to find xi, one in every list Li,such that the sum of all the xi is 0. If the lists Li are large enough,then the algorithm runs in time 2^(l/(a+1)). Note that the case a=1 corresponds to the usual birthday paradox. This Generalized BirthdayAlgorithm can be applied to solve the problem of decoding. In practice, it willapply mostly to instances of Computational SyndromeDecoding which have many solutions and, more than that,it aims at finding one solution only amongthose many solutions. I would revisit theBirthday Decoding again but this time I will changeslightly the context. So now I would assume thatthere are many solutions. I will be more specificabout how many solutions are needed when I amdone with this slide. And among those manysolutions, I only want to find one. So, I will build the listsexactly in the same manner as before. Here, I write s = s1 + s2 where I cut the targetsyndrome s arbitrarily. There is no specific reasonto do that except to have a nice symmetry and it willbe useful for higher order Generalized Birthday Algorithm. So, I have those two listsand I am interested by any element in the intersection. But since I only want onesolution to my problem, I am only interested to have oneelement in the intersection. So, I only want theintersection whose size is L²/2^(n-k) where L is the size ofboth lists L1 and L2. I am interested that thissize is larger than one. This will be the case ifI choose L = 2^((n-k)/2).
And in that case my listsare large enough to have a non-empty intersection, andthe workfactor to obtain a non-empty intersectionis L that is 2^((n-k)/2). Once this is set, itgives me the limit for the size list. I need alist of size 2^((n-k)/2) and I also know fromthe way the lists are constructed that Lcannot exceed (n/2,w/2). So, I need the condition here in red in order to be able to apply this version of Birthday Decoding. Now, I can define aGeneralized Birthday Algorithm of order 2 for decoding. So, I do exactly the samething as before except that I split everything infour parts instead of two.
Intervention
Dans la même collection
-
3.6. Stern/Dumer Algorithm
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, we will present the Stern algorithm for decoding. In fact, the idea is to combine two algorithms that we have seen before, the Lee and Brickell algorithm and the Birthday Decoding.
-
3.1. From Generic Decoding to Syndrome Decoding
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
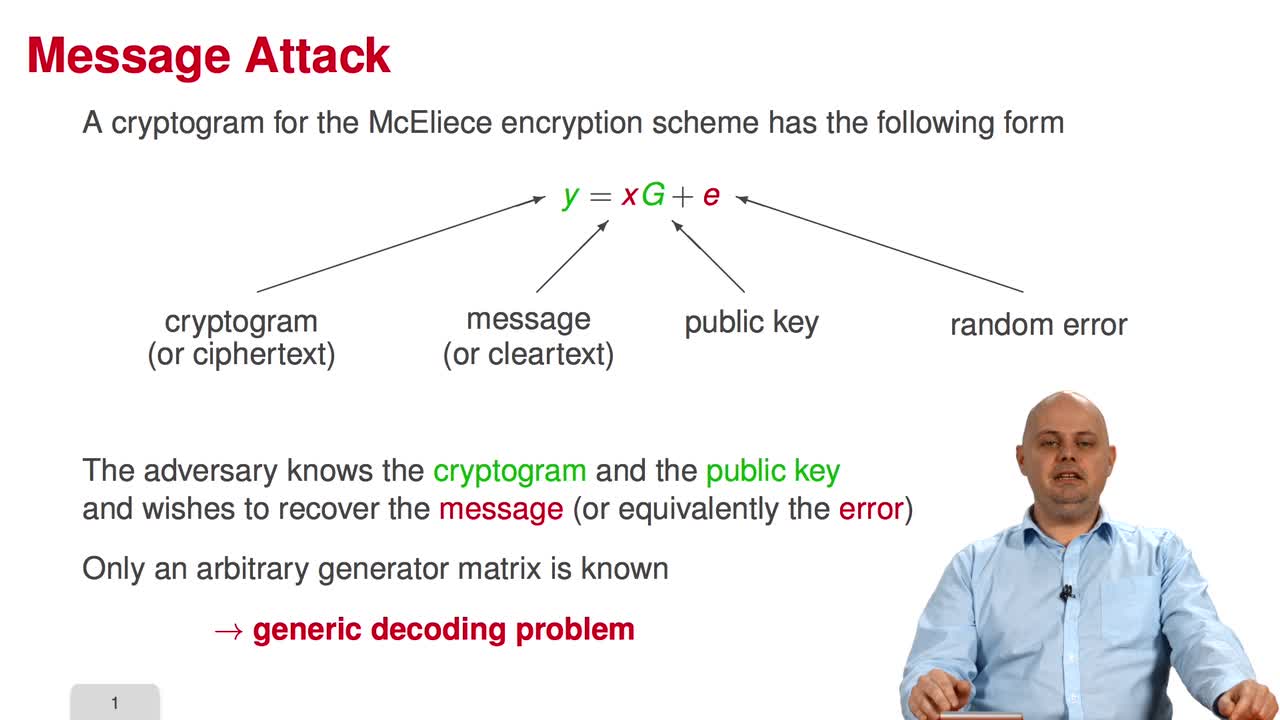
Welcome to the third week of the MOOC on code-based cryptography. This week, we will learn about message attacks. Among the ten sessions of this week, the first six will present the most essential
-
3.10. Decoding One Out of Many
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
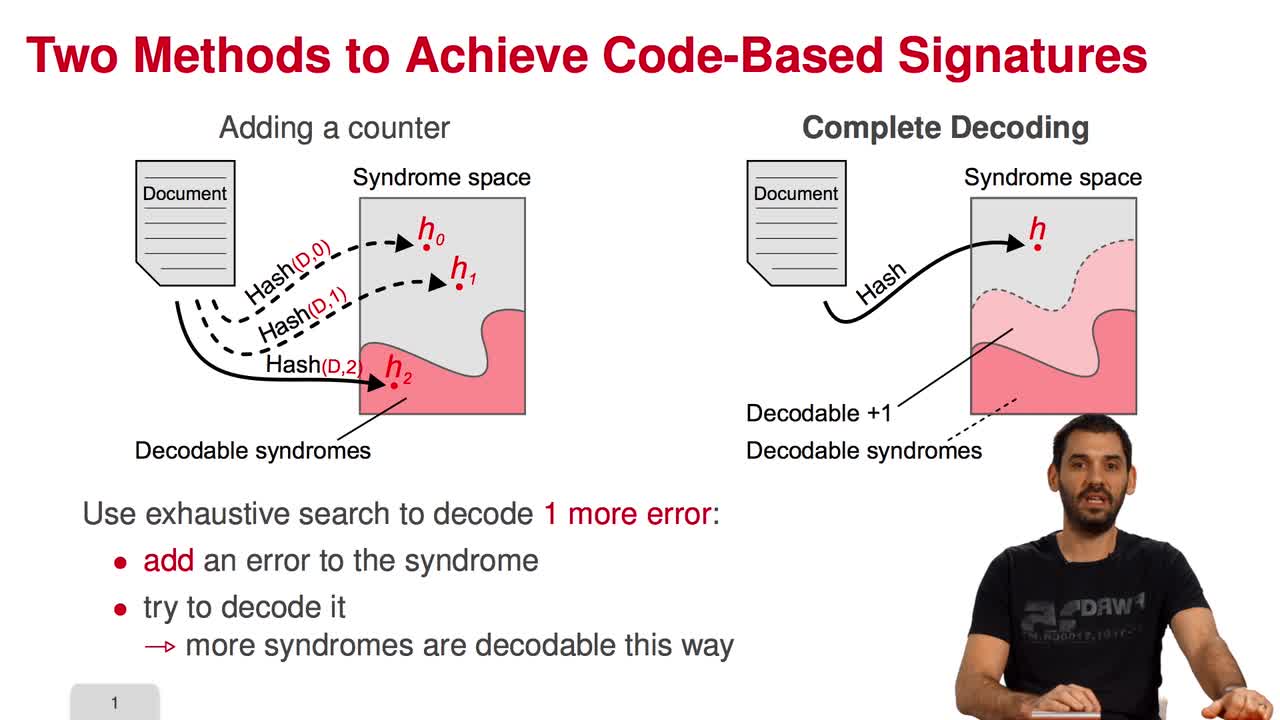
The final session of this week is devoted to Decoding One Out of Many. Decoding One Out of Many is interested in solving the following variant of Syndrome Decoding. In this variant, the only
-
3.4. Complexity Analysis
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, I will present the main technique to make the analysis of the various algorithms presented in this course. So, Information Set Decoding refers to a family of algorithms which is
-
3.7. May, Meurer, and Thomae Algorithm
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
So, with the session 7 we are entering the most advanced part of that course. The idea of what I called the Improved Birthday Decoding is to use the so-called "representation technique" introduced
-
3.2. Combinatorial Solutions: Exhaustive Search and Birthday Decoding
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, I will detail two combinatorial solutions to the decoding problem. The first one is the Exhaustive Search. To find our w columns, we will simply enumerate all the tuples j1 to jw
-
3.5. Lee and Brickell Algorithm
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this fifth session, we will study a variant of information set decoding proposed by Lee and Brickell. So, the main idea consists in relaxing the Prange algorithm to amortize the cost of the
-
3.8. Becker, Joux, May, and Meurer Algorithm
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
Now in session 8, we will present yet another evolution of information set decoding. Before presenting this improvement, we will first improve the Birthday Decoding algorithm what I call a Further
-
3.3. Information Set Decoding: the Power of Linear Algebra
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this third session, we will present the most important concept of the week: Information Set Decoding. The problem of decoding is not only a combinatorial problem. Because we are dealing with
Avec les mêmes intervenants et intervenantes
-
5.2. The Courtois-Finiasz-Sendrier (CFS) Construction
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, I am going to present the Courtois-Finiasz-Sendrier Construction of a code-based digital signature. In the previous session, we have seen that it is impossible to hash a document
-
4.6. Attack against GRS codes
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
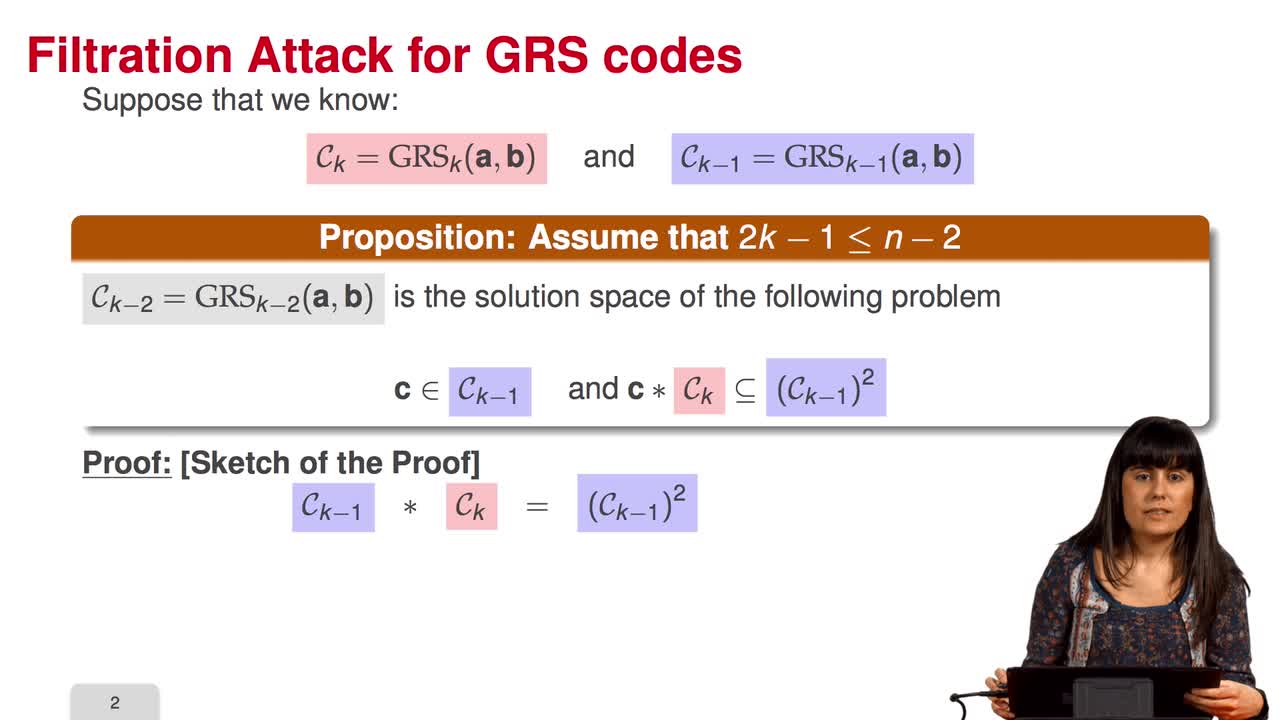
In this session we will discuss the proposal of using generalized Reed-Solomon codes for the McEliece cryptosystem. As we have already said, generalized Reed-Solomon codes were proposed in 1986 by
-
5.5. Stern’s Zero-Knowledge Identification Scheme
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, we are going to have a look at Stern’s Zero-Knowledge Identification Scheme. So, what is a Zero-Knowledge Identification Scheme? An identification scheme allows a prover to prove
-
4.9. Goppa codes still resist
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
All the results that we have seen this week doesn't mean that code based cryptography is broken. So in this session we will see that Goppa code still resists to all these attacks. So recall that
-
4.4. Attack against subcodes of GRS codes
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, we will talk about using subcodes of a Generalized Reed–Solomon code for the McEliece Cryptosystem. Recall that to avoid the attack of Sidelnikov and Shestakov, Berger and
-
5.3. Attacks against the CFS Scheme
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, we will have a look at the attacks against the CFS signature scheme. As for public-key encryption, there are two kinds of attacks against signature schemes. First kind of attack is
-
4.7. Attack against Reed-Muller codes
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, we will introduce an attack against binary Reed-Muller codes. Reed-Muller codes were introduced by Muller in 1954 and, later, Reed provided the first efficient decoding algorithm
-
5.6. An Efficient Provably Secure One-Way Function
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, we are going to see how to build an efficient provably secure one-way function from coding theory. As you know, a one-way function is a function which is simple to evaluate and
-
5.1. Code-Based Digital Signatures
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
Welcome to the last week of this MOOC on code-based cryptography. This week, we will be discussing other cryptographic constructions relying on coding theory. We have seen how to do public key
-
4.5. Error-Correcting Pairs
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
We present in this session a general decoding method for linear codes. And we will see it in an example. Let C be a generalized Reed-Solomon code of dimension k associated to the pair (c, d). Then,
-
5.4. Parallel-CFS
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
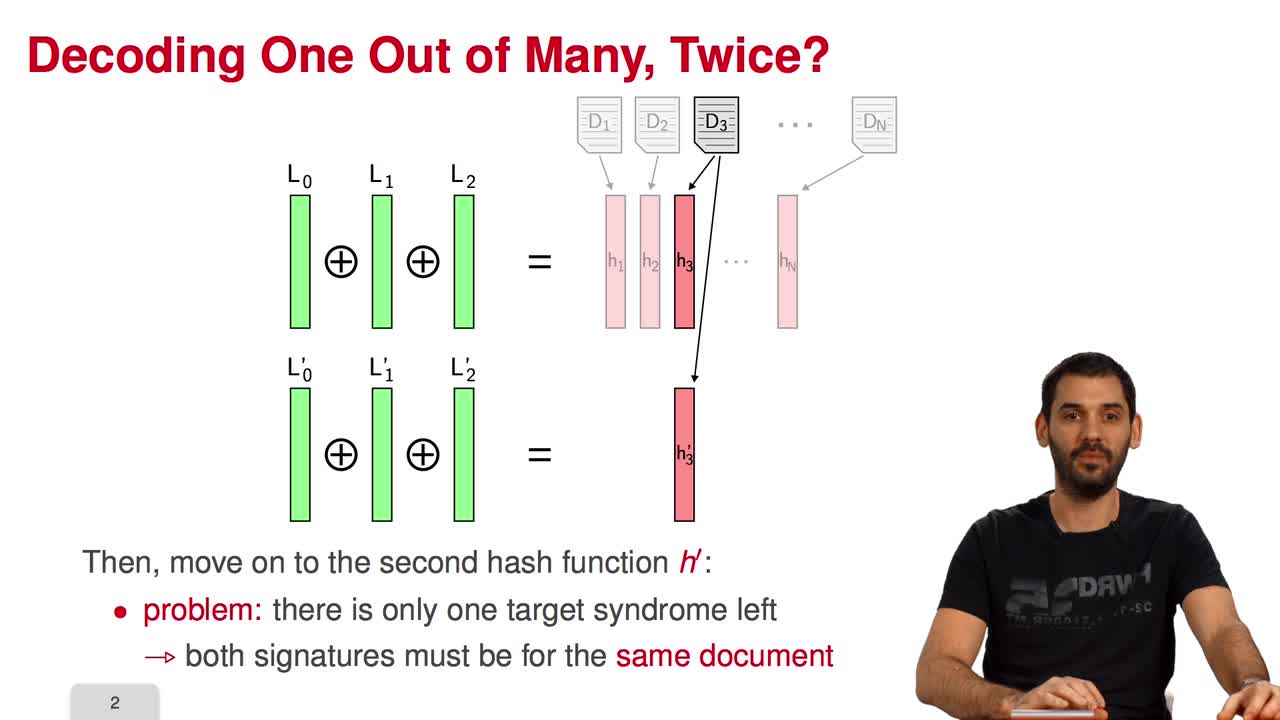
In this session, I will present a variant of the CFS signature scheme called parallel-CFS. We start from a simple question: what happens if you try to use two different hash functions and compute
-
4.8. Attack against Algebraic Geometry codes
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, we will present an attack against Algebraic Geometry codes (AG codes). Algebraic Geometry codes is determined by a triple. First of all, an algebraic curve of genus g, then a n
Sur le même thème
-
Machines algorithmiques, mythes et réalités
MAZENOD Vincent
Vincent Mazenod, informaticien, partage le fruit de ses réflexions sur l'évolution des outils numériques, en lien avec les problématiques de souveraineté, de sécurité et de vie privée...
-
Désassemblons le numérique - #Episode11 : Les algorithmes façonnent-ils notre société ?
SCHWARTZ Arnaud
LIMA PILLA Laércio
ESTéRIE Pierre
SALLET Frédéric
FERBOS Aude
ROUMANOS Rayya
CHRAIBI KADOUD Ikram
Un an après le tout premier hackathon sur les méthodologies d'enquêtes journalistiques sur les algorithmes, ce nouvel épisode part à la rencontre de différents points de vue sur les algorithmes.
-
Les machines à enseigner. Du livre à l'IA...
BRUILLARD Éric
Que peut-on, que doit-on déléguer à des machines ? C'est l'une des questions explorées par Éric Bruillard qui, du livre aux IA génératives, expose l'évolution des machines à enseigner...
-
Quel est le prix à payer pour la sécurité de nos données ?
MINAUD Brice
À l'ère du tout connecté, la question de la sécurité de nos données personnelles est devenue primordiale. Comment faire pour garder le contrôle de nos données ? Comment déjouer les pièges de plus en
-
Désassemblons le numérique - #Episode9 : Bientôt des supercalculateurs dans nos piscines ?
BEAUMONT Olivier
BOUZEL Rémi
Des supercalculateurs feraient-ils bientôt leur apparition dans les piscines municipales pour les chauffer ? Réponses d'Olivier Beaumont, responsable de l'équipe-projet Topal, et Rémi Bouzel,
-
Des systèmes de numération pour le calcul modulaire
BAJARD Jean-Claude
Le calcul modulaire est utilisé dans de nombreuses applications des mathématiques, telles que la cryptographie...
-
Projection methods for community detection in complex networks
LITVAK Nelly
Community detection is one of most prominent tasks in the analysis of complex networks such as social networks, biological networks, and the world wide web. A community is loosely defined as a group
-
Lara Croft. doing fieldwork under surveillance
DALL'AGNOLA Jasmin
Lara Croft. Doing Fieldwork Under Surveillance Intervention de Jasmin Dall'Agnola (The George Washington University), dans le cadre du Colloque coorganisé par Anders Albrechtslund, professeur en
-
Containing predictive tokens in the EU
CZARNOCKI Jan
Containing Predictive Tokens in the EU – Mapping the Laws Against Digital Surveillance, intervention de Jan Czarnocki (KU Leuven), dans le cadre du Colloque coorganisé par Anders Albrechtslund,
-
Inauguration de l'exposition - Vanessa Vitse : Nombres de Sophie Germain et codes secrets
VITSE Vanessa
Exposé de Vanessa Vitse (Institut Fourier) : Nombres de Sophie Germain et codes secrets
-
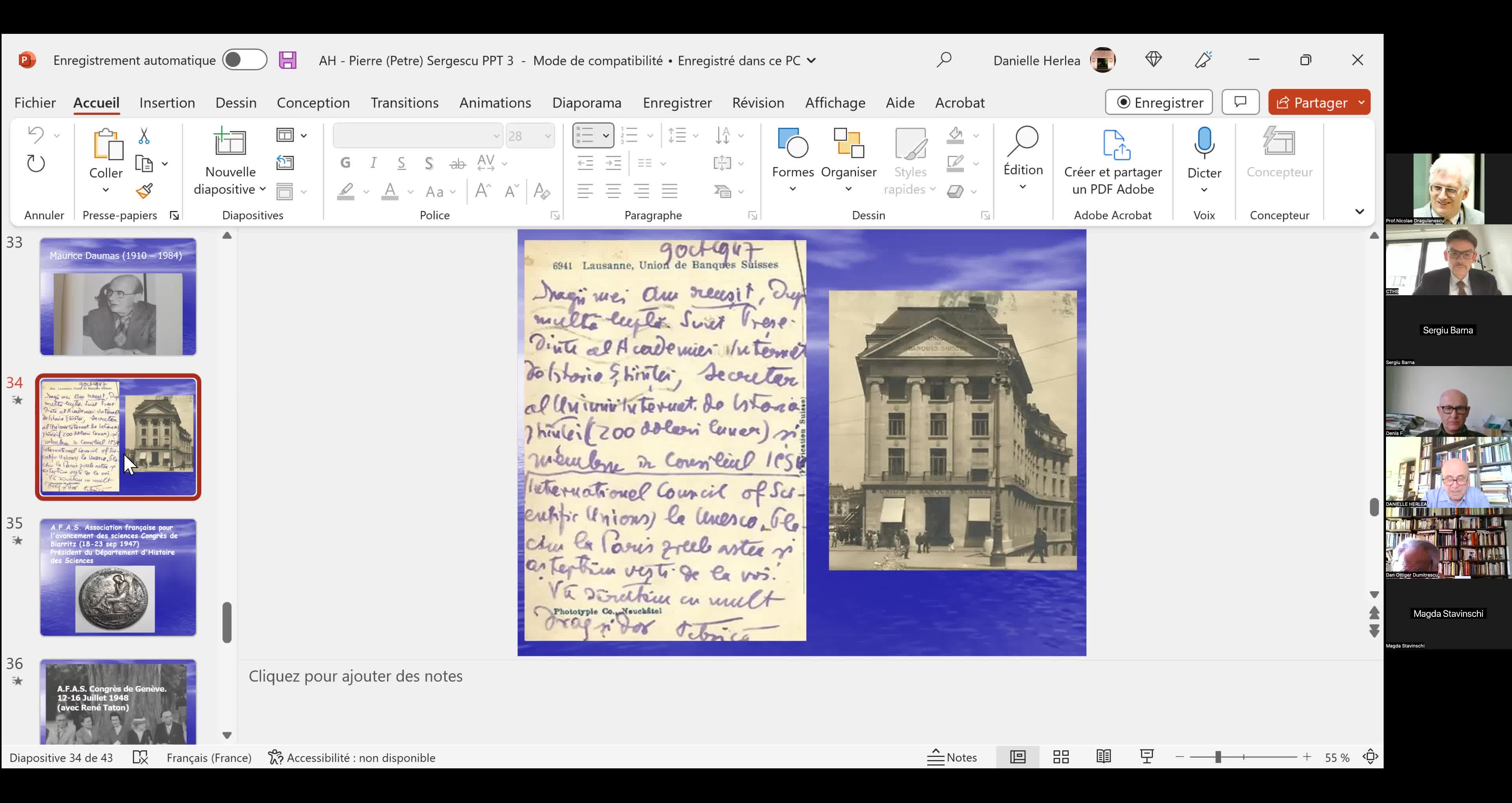
"Le mathématicien Petre (Pierre) Sergescu, historien des sciences, personnalité du XXe siècle"
HERLéA Alexandre
Alexandre HERLEA est membre de la section « Sciences, histoire des sciences et des techniques et archéologie industrielle » du CTHS. Professeur émérite des universités, membre effectif de l'Académie
-
Ivan Murit - Processus de création d'images
MURIT Ivan
Je vais présenter une manière décalée d'aborder les outils d'impression. Pour cela nous ne partirons pas de l'envie d'imprimer une image préexistante, mais d'avant cela : comment se crée une forme