Notice
2.1. Formal Definition
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
Welcome to the second week of this MOOC entitledCode-Based Cryptography. This week, we will talk in detailabout the McEliece cryptosystem. First, in this session, wewill describe formally the McEliece and theNiederreiter systems, which are the principal public-key schemes,based on error-correcting code. Let K be a securityparameter. An encryption schemeis defined by thefollowing spaces: the space of all possible messages, thespace of all ciphertexts, thespace of the public-keys, andthe space of the secret-keys.Then, we need to definethe following algorithms.A key generationalgorithm, which is a randomized algorithm that outputs apublic-key and a secret-key;this algorithm should runin expected polynomial time.
An encryption algorithm,which is also a randomized algorithm that takes amessage and the public-key and outputs a ciphertext;this algorithm runs also inexpected polynomial time.And a decryption algorithm,which is an algorithm thattakes a ciphertext and asecret-key, and outputs theoriginal plaintext ordeclares a failure; this algorithmruns in polynomial time.It is required that thedecryption of the ciphertext isagain the plaintext, and wedemand that the fasten attack on the system requires atleast 2^k bit operations.In 1978, McElieceintroduced the first public-keycryptosystem, as we have alreadyseen, based on error-correcting codes.The security of this schemeis based on two intractableproblems: the hardness ofdecoding, and the problem ofdistinguishing a codewith a prescribed structure.This property makesthis scheme an interesting candidate forpost-quantum cryptography. Another advantage consists of its fastencryption and decryption algorithms. But the main drawback isthe large size of the keys. We will use as public-key,a large generator matrix.
Intervention
Dans la même collection
-
2.6. Reducing the Key Size
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
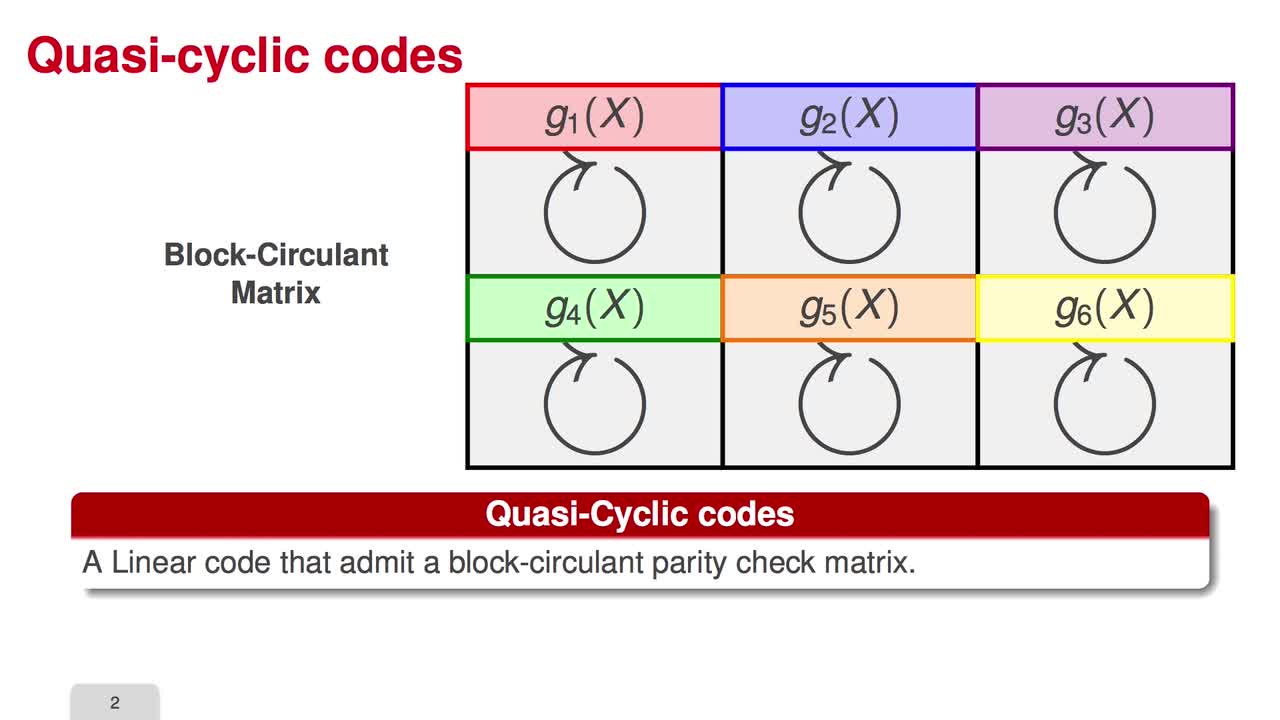
In the next three sessions, I will explain how to reduce the key size of code-based cryptosystem. Circulant matrices are the central point in many attempts to reduce the key size of code-based
-
2.9. Implementation
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
This is the last session of the second week. The cryptography community has different options for using public key cryptosystems, among others, they have RSA or DSA. But … McEliece has the same
-
2.4. Notions of Security
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, we will study the notion of security of public-key scheme. A public-key scheme is one-way if the probability of success of any adversary running in polynomial time is negligible.
-
2.7. Reducing the Key Size - LDPC codes
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
LDPC codes have an interesting feature: they are free of algebraic structure. We will study in detail this proposal for the McEliece cryptosystem in this session. LDPC codes were originally
-
2.2. Security-Reduction Proof
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
Welcome to the second session. We will talk about the security-reduction proof. The security of a given cryptographic algorithm is reduced to the security of a known hard problem. To prove that a
-
2.5. Critical Attacks - Semantic Secure Conversions
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
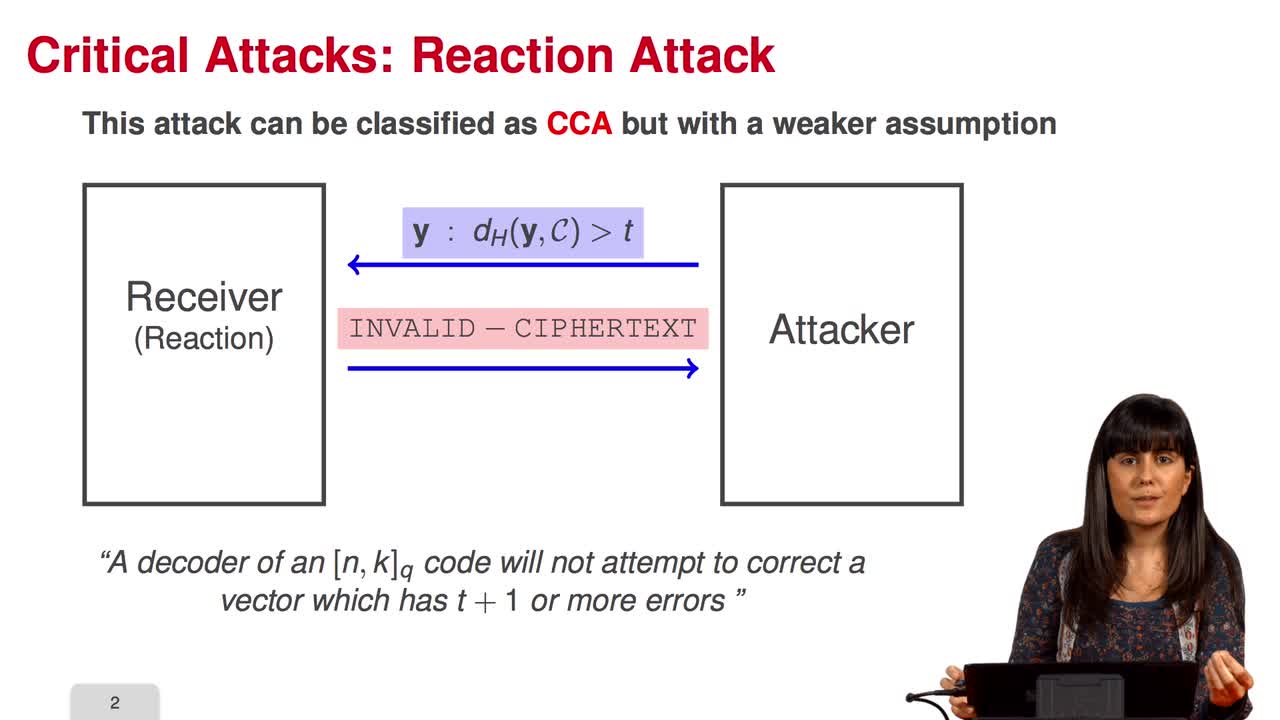
In this session, we will study critical attacks against the public-key cryptosystem. The partial knowledge on the plaintext reduces drastically the computational cost of the attack to the McEliece
-
2.8. Reducing the Key Size - MDPC codes
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
This is the last session where we will talk about reducing the key size. Here we will introduce the MDPC codes. In 2012, the MDPC codes were proposed for the McEliece schemes. An MDPC code is a
-
2.3. McEliece Assumptions
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
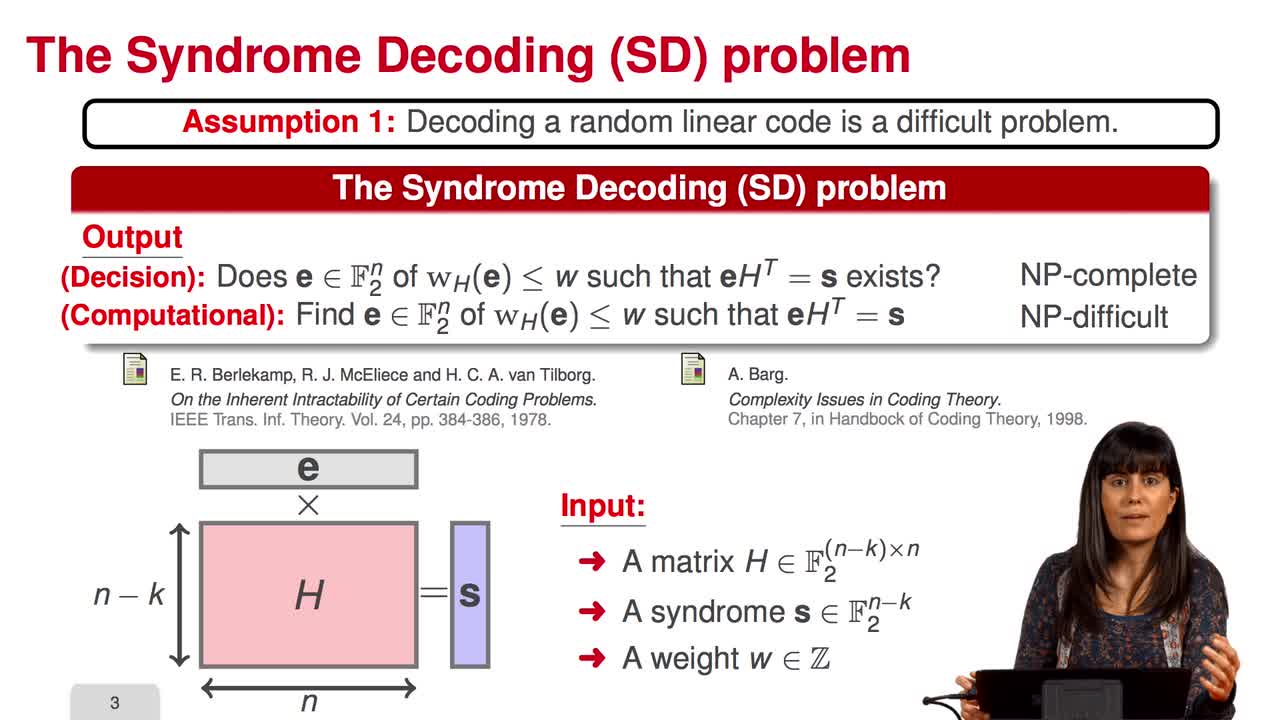
In this session, we will talk about McEliece assumptions. The security of the McEliece scheme is based on two assumptions as we have already seen: the hardness of decoding a random linear code and
Avec les mêmes intervenants et intervenantes
-
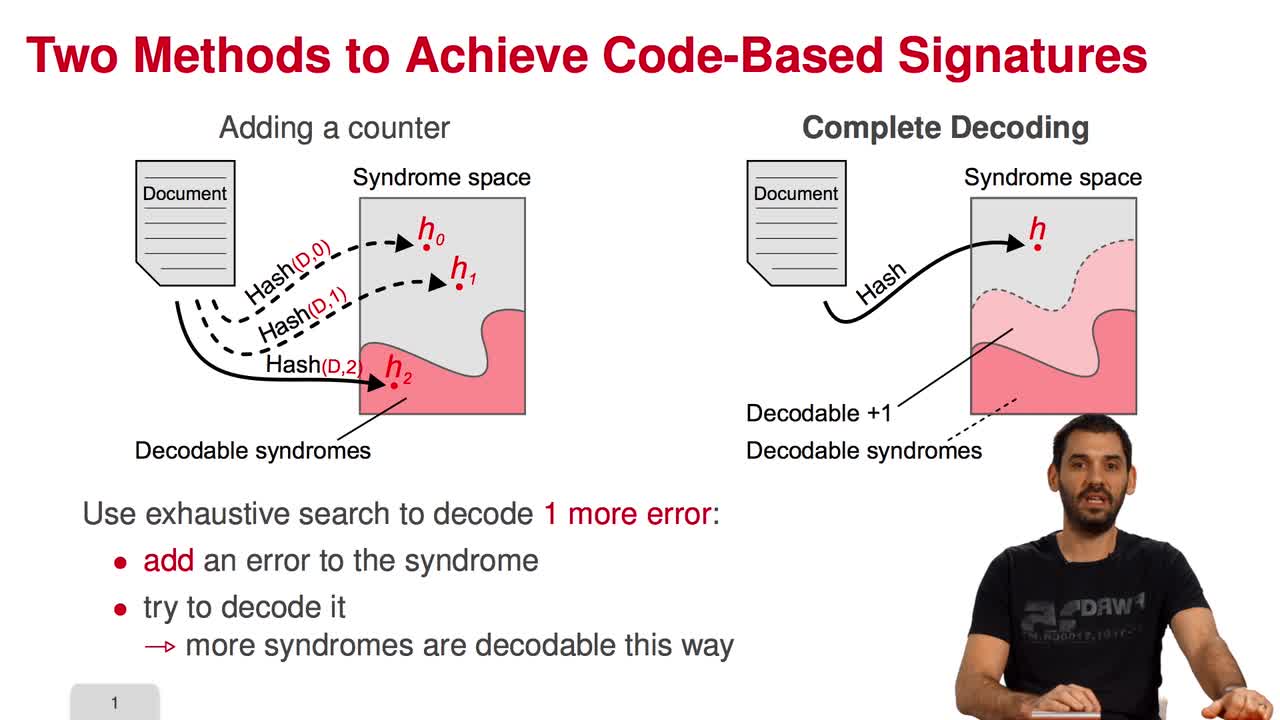
5.1. Code-Based Digital Signatures
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
Welcome to the last week of this MOOC on code-based cryptography. This week, we will be discussing other cryptographic constructions relying on coding theory. We have seen how to do public key
-
4.5. Error-Correcting Pairs
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
We present in this session a general decoding method for linear codes. And we will see it in an example. Let C be a generalized Reed-Solomon code of dimension k associated to the pair (c, d). Then,
-
5.4. Parallel-CFS
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
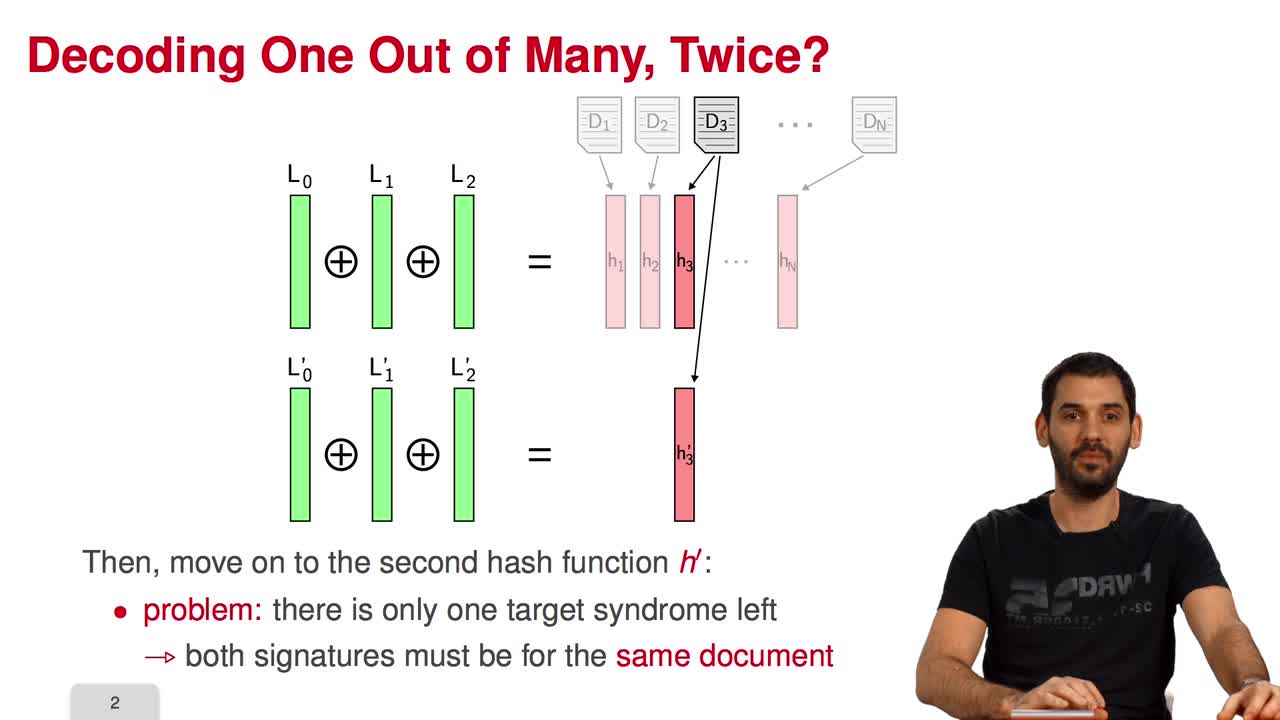
In this session, I will present a variant of the CFS signature scheme called parallel-CFS. We start from a simple question: what happens if you try to use two different hash functions and compute
-
4.8. Attack against Algebraic Geometry codes
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, we will present an attack against Algebraic Geometry codes (AG codes). Algebraic Geometry codes is determined by a triple. First of all, an algebraic curve of genus g, then a n
-
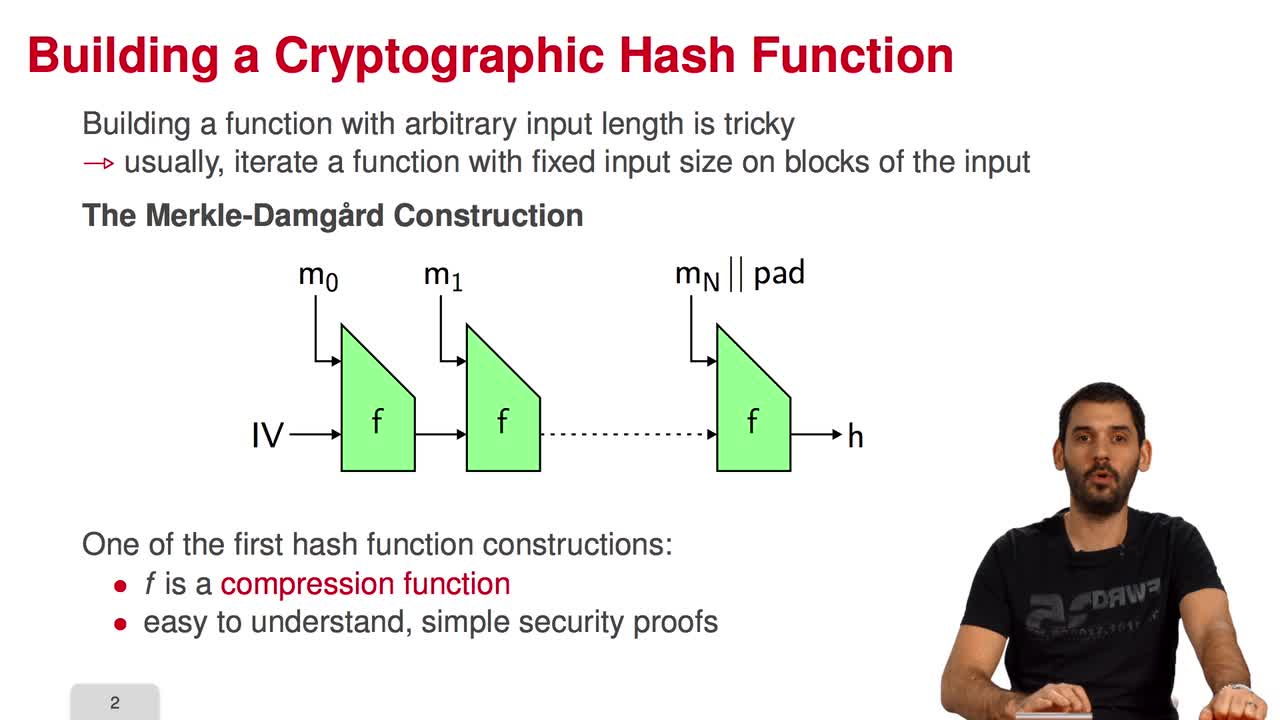
5.7. The Fast Syndrome-Based (FSB) Hash Function
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In the last session of this week, we will have a look at the FSB Hash Function which is built using the one-way function we saw in the previous session. What are the requirements for a
-
5.2. The Courtois-Finiasz-Sendrier (CFS) Construction
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, I am going to present the Courtois-Finiasz-Sendrier Construction of a code-based digital signature. In the previous session, we have seen that it is impossible to hash a document
-
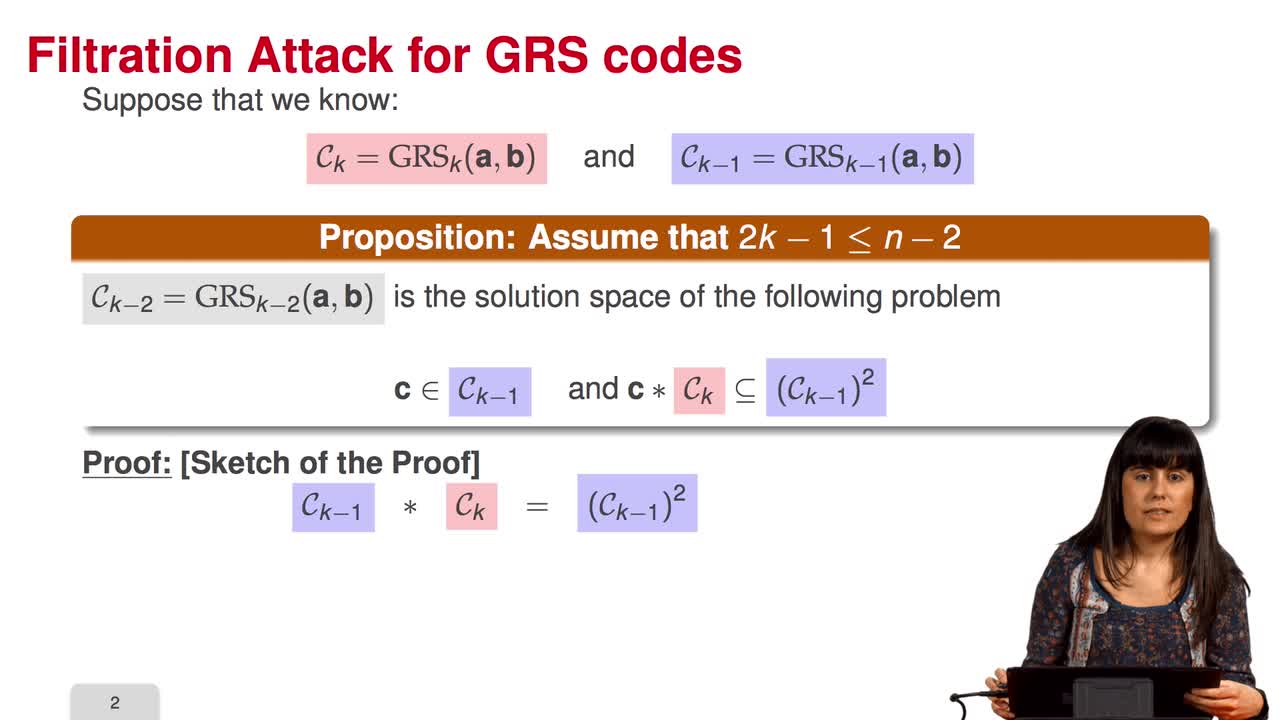
4.6. Attack against GRS codes
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session we will discuss the proposal of using generalized Reed-Solomon codes for the McEliece cryptosystem. As we have already said, generalized Reed-Solomon codes were proposed in 1986 by
-
5.5. Stern’s Zero-Knowledge Identification Scheme
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, we are going to have a look at Stern’s Zero-Knowledge Identification Scheme. So, what is a Zero-Knowledge Identification Scheme? An identification scheme allows a prover to prove
-
4.9. Goppa codes still resist
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
All the results that we have seen this week doesn't mean that code based cryptography is broken. So in this session we will see that Goppa code still resists to all these attacks. So recall that
-
4.4. Attack against subcodes of GRS codes
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, we will talk about using subcodes of a Generalized Reed–Solomon code for the McEliece Cryptosystem. Recall that to avoid the attack of Sidelnikov and Shestakov, Berger and
-
5.3. Attacks against the CFS Scheme
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, we will have a look at the attacks against the CFS signature scheme. As for public-key encryption, there are two kinds of attacks against signature schemes. First kind of attack is
-
4.7. Attack against Reed-Muller codes
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, we will introduce an attack against binary Reed-Muller codes. Reed-Muller codes were introduced by Muller in 1954 and, later, Reed provided the first efficient decoding algorithm
Sur le même thème
-
Quel est le prix à payer pour la sécurité de nos données ?
MINAUD Brice
À l'ère du tout connecté, la question de la sécurité de nos données personnelles est devenue primordiale. Comment faire pour garder le contrôle de nos données ? Comment déjouer les pièges de plus en
-
Des systèmes de numération pour le calcul modulaire
BAJARD Jean-Claude
Le calcul modulaire est utilisé dans de nombreuses applications des mathématiques, telles que la cryptographie...
-
Inauguration de l'exposition - Vanessa Vitse : Nombres de Sophie Germain et codes secrets
VITSE Vanessa
Exposé de Vanessa Vitse (Institut Fourier) : Nombres de Sophie Germain et codes secrets
-
"Le mathématicien Petre (Pierre) Sergescu, historien des sciences, personnalité du XXe siècle"
HERLéA Alexandre
Alexandre HERLEA est membre de la section « Sciences, histoire des sciences et des techniques et archéologie industrielle » du CTHS. Professeur émérite des universités, membre effectif de l'Académie
-
Retour d'expérience sur l'utilisation croisée de plusieurs archives de fouilles
TUFFéRY Christophe
Dans le cadre d'une thèse de doctorat engagée depuis 2019, une étude historiographique et épistémologique des effets des dispositifs numériques sur l'archéologie et sur les archéologues au cours des
-
Information Structures for Privacy and Fairness
PALAMIDESSI Catuscia
Information Structures for Privacy and Fairness
-
AI and Human Decision-Making: An Interdisciplinary Perspective
CASTELLUCCIA Claude
This seminar will talk about some of the privacy risks of these systems and will describe some recent attacks. It will also discuss why they sometimes fail to deliver. Finally, we will also show that
-
Webinaire sur la rédaction des PGD
LOUVET Violaine
Rédaction des Plans de Gestion de Données (PGD) sous l’angle des besoins de la communauté mathématique.
-
Alexandre Booms : « Usage de matériel pédagogique adapté en géométrie : une transposition à interro…
« Usage de matériel pédagogique adapté en géométrie : une transposition à interroger ». Alexandre Booms, doctorant (Université de Reims Champagne-Ardenne - Cérep UR 4692)
-
Présentation de la rencontre. A l’heure du numérique « Quelles mesures pour la mesure ? ». Le relev…
BADIE Alain
TARDY Dominique
MALMARY Jean-Jacques
ZUGMEYER Stéphanie
Rencontre-Atelier de l'ANR Ornementation Architecturale des Gaules. À l’heure du numérique, « Quelles mesures pour la mesure ? ». Le relevé des blocs d’architecture décorés et l’apport des outils
-
Photogrammétrie : Performances et limitations
EGELS Yves
Rencontre-Atelier de l'ANR Ornementation Architecturale des Gaules. À l’heure du numérique, « Quelles mesures pour la mesure ? ». Le relevé des blocs d’architecture décorés et l’apport des outils
-
Relever et publier des blocs d’architecture : objectifs et méthodes
BADIE Alain
Rencontre-Atelier de l'ANR Ornementation Architecturale des Gaules. À l’heure du numérique, « Quelles mesures pour la mesure ? ». Le relevé des blocs d’architecture décorés et l’apport des outils