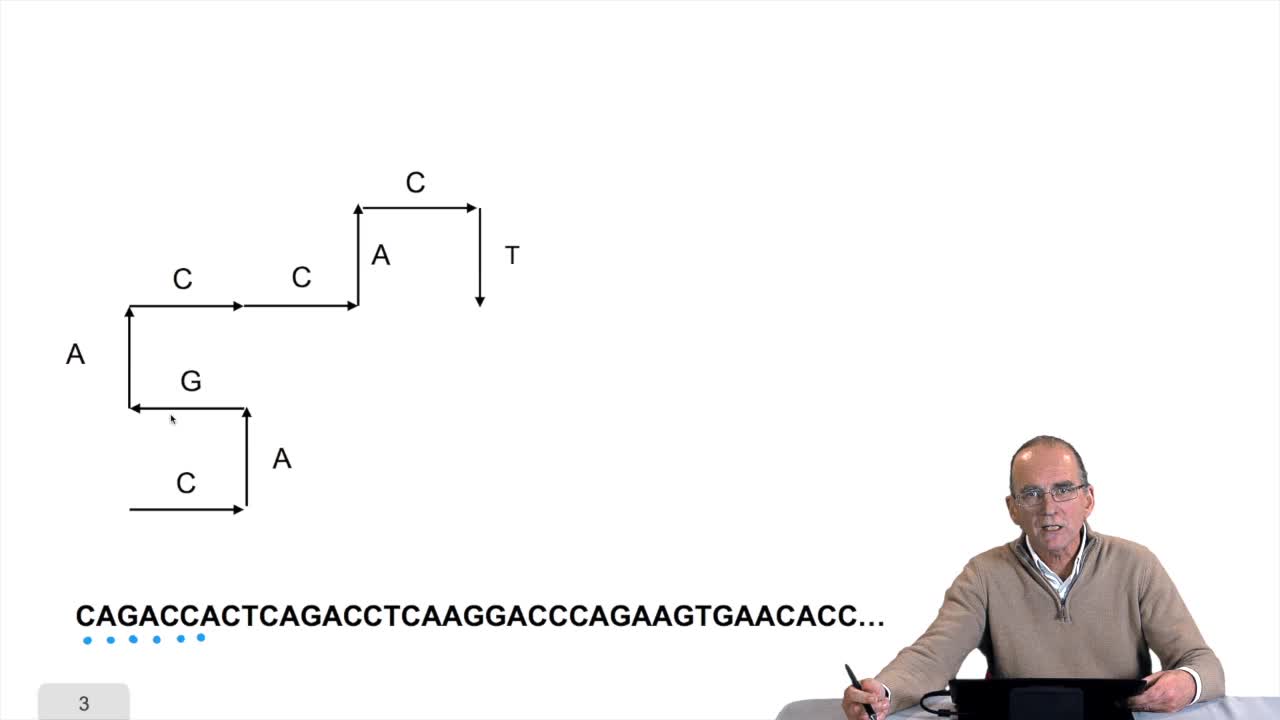Notice
5.2. L’arbre, objet abstrait
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
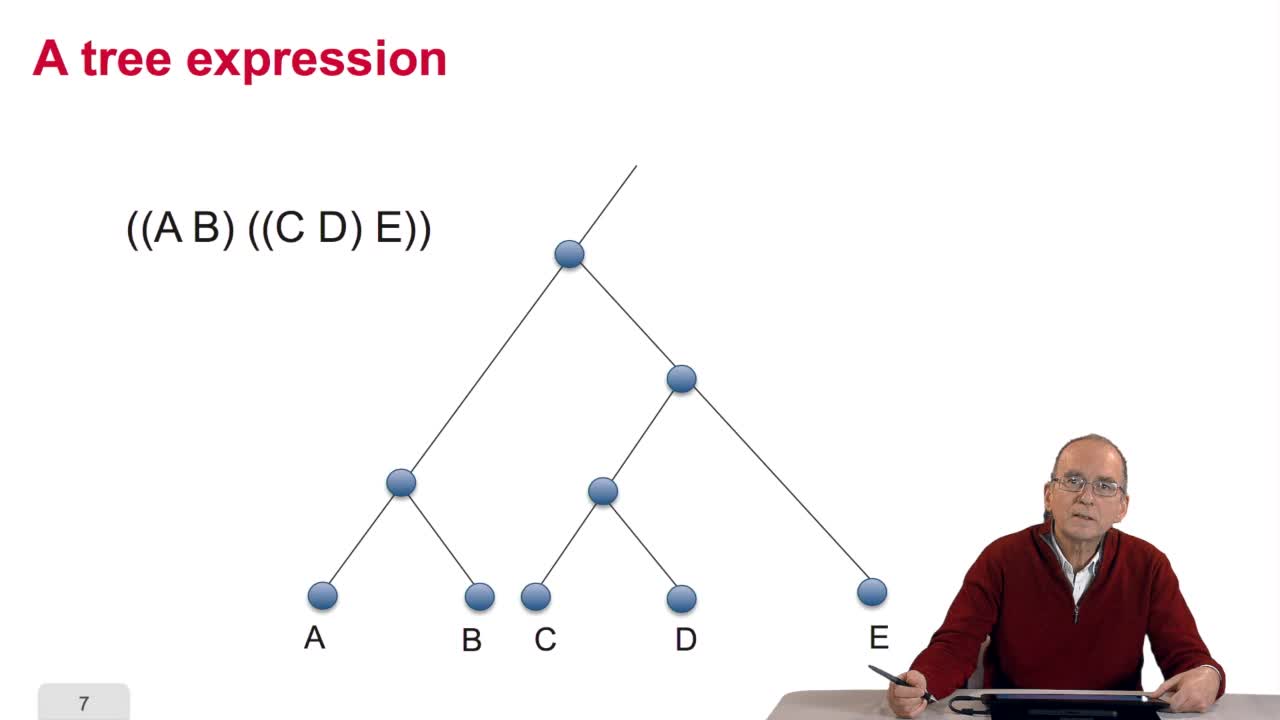
Vous l'aurez compris un arbre phylogénétique est un arbre abstrait qui n'a qu'un lointain rapport métaphorique avec un véritable arbre. L'arbre des bio-informaticiens et des informaticiens se dessinent du reste dans l'autre sens. C'est-à-dire que si on retrouve bien effectivement des branches qui connectent des noeuds, on a un noeud qui est la racine et qui est situé tout en haut et on situe en bas généralement par convention, les feuilles qu'on appelle également noeuds terminaux. Pour décrire un arbre, on peut utiliser une expression parenthésée, dont la logique s'impose assez rapidement. Voilà ici l'expression parenthésée correspondant à cette structure d'arbres. On voit cette sous-expression correspondre à ce sous-arbre. Très logiquement, cette expression correspond à ce sous-arbre. Et donc, cette expression-là correspond au sous-arbre incluant celui-ci, plus le noeud E. Et l'arbre tout entier est de noter par cette expression. Nous avons donc là un moyen non ambigu de noter une topologie, une structure d'arbre. Bien entendu, cette topologie d'arbres ne change pas suivant la manière dont on le dessine. On peut également avoir des expressions parenthésées différentes mais qui sont équivalentes du point de vue descriptif. Cette expression parenthésée est strictement équivalente à celle-ci. Elle décrit la même structure d'arbres. De même, les arbres peuvent prendre plusieurs apparences, suivant le style de dessin utilisé, la topologie reste la même. Cette manière de représenter les arbres est de loin préférée par les biologistes...
Intervention / Responsable scientifique
Dans la même collection
-
5.3. Remplir un tableau de distances
RechenmannFrançoisParmentelatThierryPour tenter de construire l'arbre phylogénétique d'un ensemble d'espèces, nous allons utiliser les données et génotypique ou des données génotypiques disponibles sur ces espèces. Plus clairement, nous
-
5.6. La diversité des algorithmes informatiques
RechenmannFrançoisParmentelatThierryNous n'avons vu dans ce cours qu'un exemple extrêmement réduit d'algorithme bio informatique. Il existe en effet une très grande diversité de ces algorithmes bio informatiques qui sont motivés par l
-
5.4. L’algorithme UPGMA
RechenmannFrançoisParmentelatThierryL'algorithme, que nous allons étudier pour la reconstruction d'arbres phylogénétiques à partir des distances, s'appelle UPGMA. Un nom plutôt compliqué pour une méthode qui est plutôt simple. Et même,
-
5.7. Les applications en microbiologie
RechenmannFrançoisParmentelatThierryUne très grande diversité, on l'a vu, d'algorithmes en bio-informatique, motivé par la résolution de problèmes différents. Ces algorithmes, ces recherches en bio-informatique, s'appuient sur des
-
5.1. L’arbre des espèces
RechenmannFrançoisParmentelatThierryDans cette cinquième et dernière partie de notre cours sur le génome et les algorithmes, qui se veut une introduction à l'analyse informatique de l'information génétique, nous regarderons de plus près
-
5.5. Quand les différences sont trompeuses
RechenmannFrançoisParmentelatThierryIl y a plusieurs raisons pour lesquelles la méthode UPGMA, que nous venons de voir, se révèle simpliste. L'une des raisons par exemple, c'est pourquoi quand on recalcule les distances, quand on a
Avec les mêmes intervenants et intervenantes
-
1.8. Compressing the DNA walk
RechenmannFrançoisWe have written the algorithm for the circle DNA walk. Just a precision here: the kind of drawing we get has nothing to do with the physical drawing of the DNA molecule. It is a symbolic
-
2.7. The algorithm design trade-off
RechenmannFrançoisWe saw how to increase the efficiencyof our algorithm through the introduction of a data structure. Now let's see if we can do even better. We had a table of index and weexplain how the use of these
-
3.4. Predicting all the genes in a sequence
RechenmannFrançoisWe have written an algorithm whichis able to locate potential genes on a sequence but only on one phase because we are looking triplets after triplets. Now remember that the genes maybe located on
-
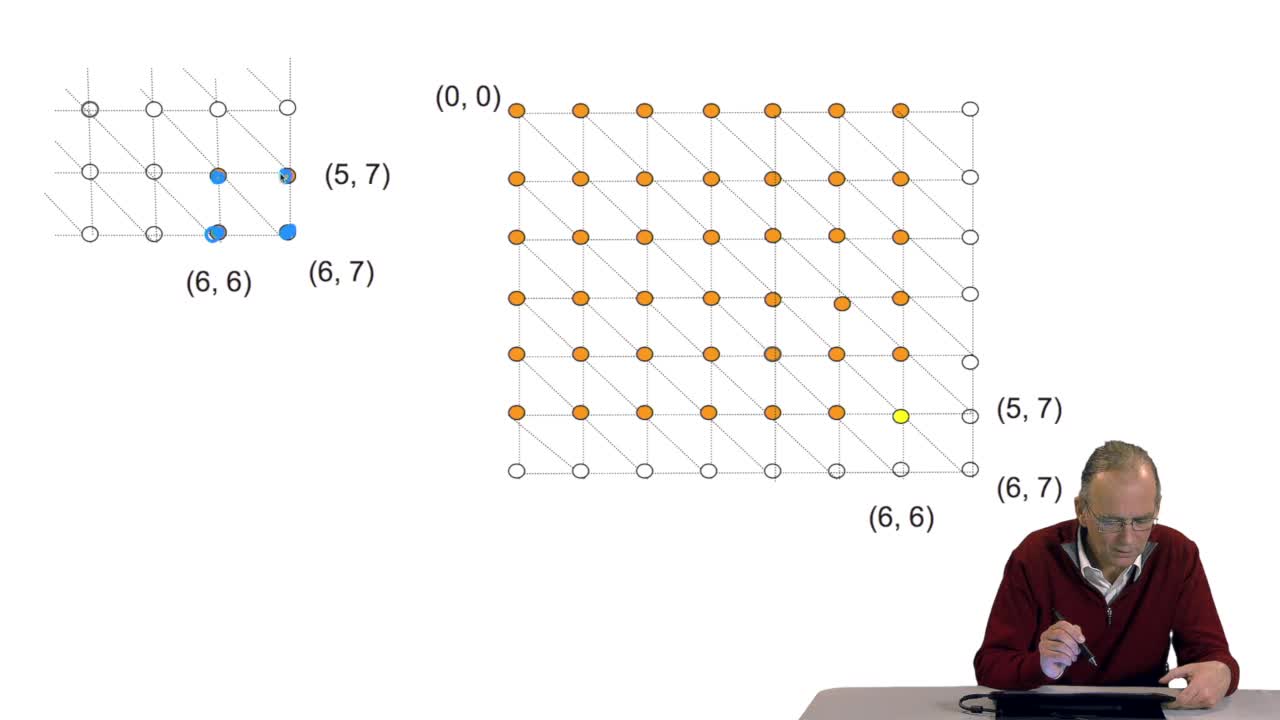
4.7. Alignment costs
RechenmannFrançoisWe have seen how we can compute the cost of the path ending on the last node of our grid if we know the cost of the sub-path ending on the three adjacent nodes. It is time now to see more deeply why
-
4.9. Recursion can be avoided: an iterative version
RechenmannFrançoisWe have written a recursive function to compute the optimal path that is an optimal alignment between two sequences. Here all the examples I gave were onDNA sequences, four letter alphabet. OK. The
-
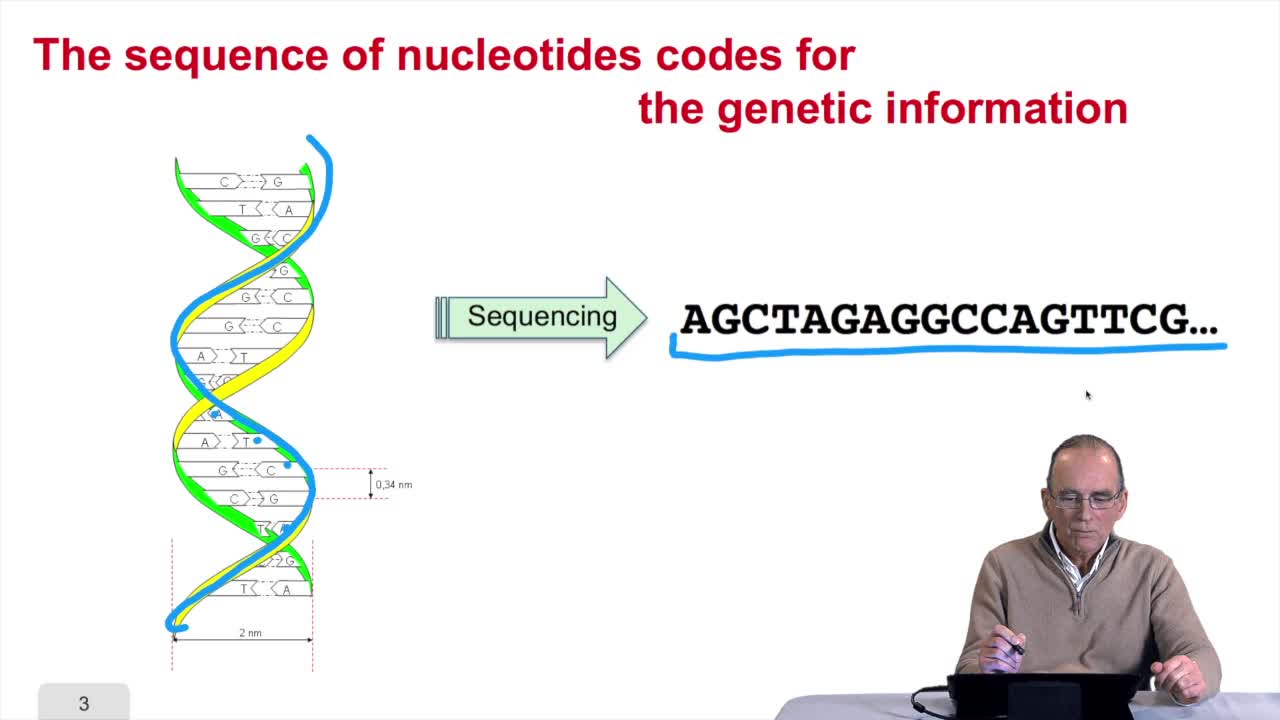
1.3. DNA codes for genetic information
RechenmannFrançoisRemember at the heart of any cell,there is this very long molecule which is called a macromolecule for this reason, which is the DNA molecule. Now we will see that DNA molecules support what is called
-
2.1. The sequence as a model of DNA
RechenmannFrançoisWelcome back to our course on genomes and algorithms that is a computer analysis ofgenetic information. Last week we introduced the very basic concept in biology that is cell, DNA, genome, genes
-
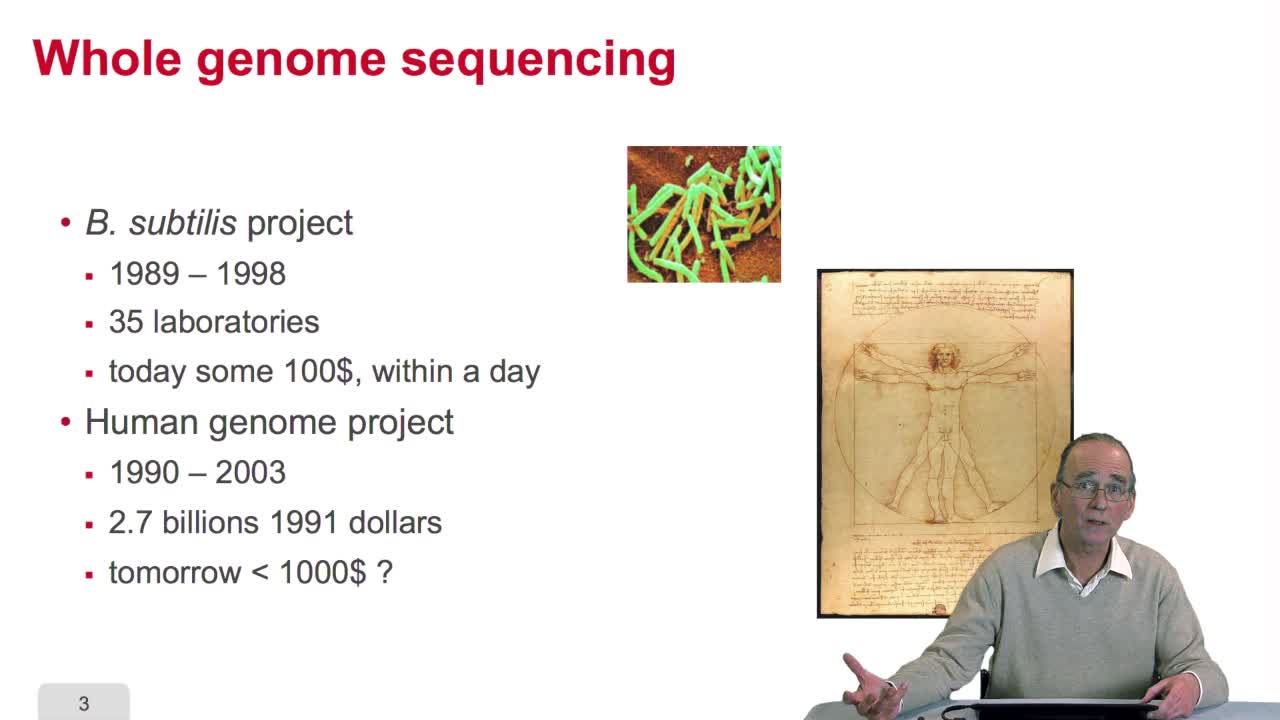
2.9. Whole genome sequencing
RechenmannFrançoisSequencing is anexponential technology. The progresses in this technologyallow now to a sequence whole genome, complete genome. What does it mean? Well let'stake two examples: some twenty years ago,
-
3.7. Index and suffix trees
RechenmannFrançoisWe have seen with the Boyer-Moore algorithm how we can increase the efficiency of spin searching through the pre-processing of the pattern to be searched. Now we will see that an alternative way of
-
4.4. Aligning sequences is an optimization problem
RechenmannFrançoisWe have seen a nice and a quitesimple solution for measuring the similarity between two sequences. It relied on the so-called hammingdistance that is counting the number of differencesbetween two
-
5.2. The tree, an abstract object
RechenmannFrançoisWhen we speak of trees, of species,of phylogenetic trees, of course, it's a metaphoric view of a real tree. Our trees are abstract objects. Here is a tree and the different components of this tree.
-
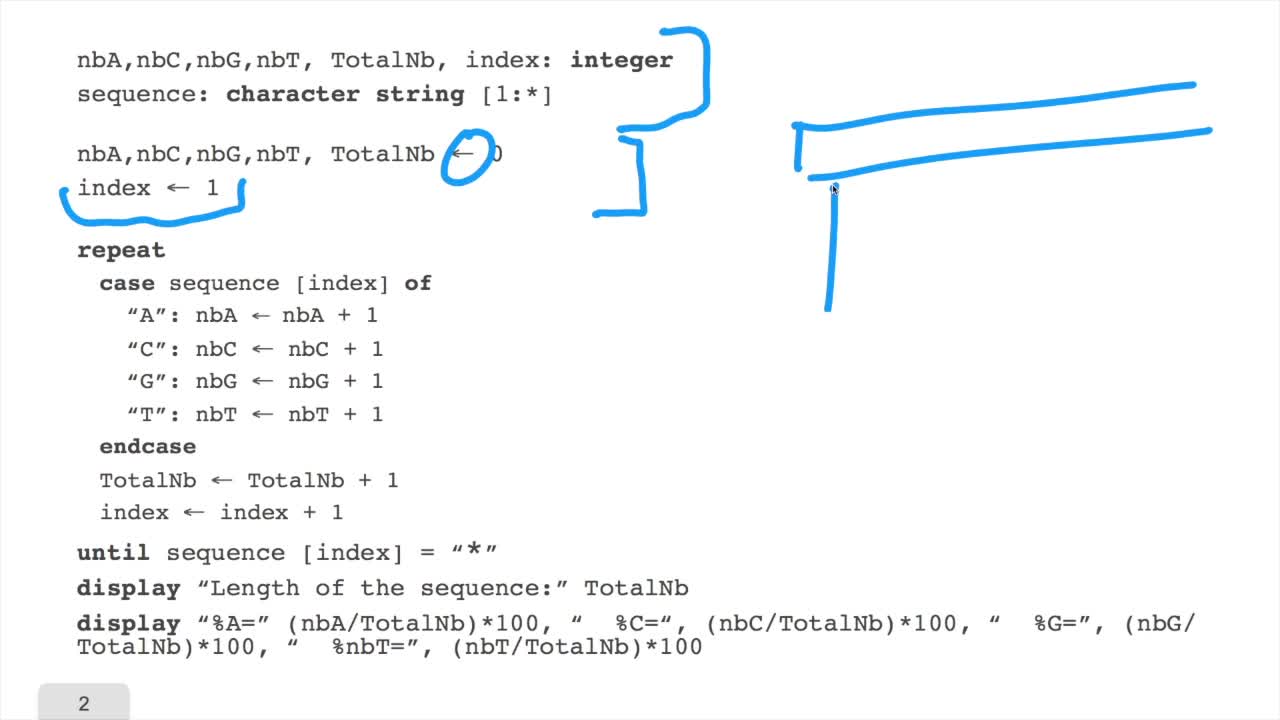
1.6. GC and AT contents of DNA sequence
RechenmannFrançoisWe have designed our first algorithmfor counting nucleotides. Remember, what we have writtenin pseudo code is first declaration of variables. We have several integer variables that are variables which
Sur le même thème
-
La voix, une donnée identifiante à protéger
VincentEmmanuelEmmanuel Vincent, chercheur au Centre Inria de l'Université de Lorraine et au Loria (Laboratoire lorrain de recherche en informatique et ses applications), présente sa recherche sur l'anonymisation de
-
Podcast 1/4 d'heure avec : Emmanuel Vincent, chercheur au Centre Inria de l'Université de Lorraine …
VincentEmmanuelRencontre avec Emmanuel Vincent - chercheur au Centre Inria de l'Université de Lorraine et Loria (Laboratoire lorrain de recherche en informatique et ses applications).
-
Stockage de données numériques sur ADN synthétique : Introduction au domaine
AntoniniMarcDuprazElsaLavenierDominiquePrésentation globale des différentes étapes du stockage de données sur des molécules d'ADN synthétique
-
Stockage de données numériques sur ADN synthétique : Production des données: synthèse, séquençage
LavenierDominiqueBarbryPascalDescription des opérations d'écriture et de lecture des molécules d'ADN : synthèse et séquençage.
-
Stockage de données numériques sur ADN synthétique : Reconstruction des données
LavenierDominiqueTraitement des données après séquençage
-
Stockage de données numériques sur ADN synthétique : Codage Canal
DuprazElsaTechniques de codage pour le stockage de données sur ADN
-
Stockage de données numériques sur ADN synthétique : Codage Source
AntoniniMarcCodage source pour le stockage de données sur ADN synthétique
-
Stockage de données numériques sur ADN synthétique : Théorie de l'information
Kas HannaSergeQuelle quantité d'information peut-on stocker et récupérer de manière fiable dans l'ADN ?
-
The tree of life
AbbySophieLes Rencontres Exobiologiques pour Doctorants (RED) sont une école de formation sur les « bases de l'astrobiologie ». L’édition 2025 s’est tenue du 16 au 21 mars au Parc Ornithologique du Teich.
-
Machines algorithmiques, mythes et réalités
MazenodVincentVincent Mazenod, informaticien, partage le fruit de ses réflexions sur l'évolution des outils numériques, en lien avec les problématiques de souveraineté, de sécurité et de vie privée...
-
Désassemblons le numérique - #Episode11 : Les algorithmes façonnent-ils notre société ?
SchwartzArnaudLima PillaLaércioEstériePierreSalletFrédéricFerbosAudeRoumanosRayyaChraibi KadoudIkramUn an après le tout premier hackathon sur les méthodologies d'enquêtes journalistiques sur les algorithmes, ce nouvel épisode part à la rencontre de différents points de vue sur les algorithmes.
-
Les machines à enseigner. Du livre à l'IA...
BruillardÉricQue peut-on, que doit-on déléguer à des machines ? C'est l'une des questions explorées par Éric Bruillard qui, du livre aux IA génératives, expose l'évolution des machines à enseigner...