Chapitres
- Présentation02'08"
- Introduction03'48"
- Les définitions comme aboutissement10'10"
- Les définitions comme commencement11'17"
- Les définitions comme piège17'12"
- Convolution, ondelette, fractale04'17"
- Conclusion04'47"
- Questions: partie 109'37"
- Questions: partie 214'33"
Notice
Nécessité et pièges des définitions mathématiques
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
D'où viennent et à quoi servent les définitions mathématiques ? En quoi sont-elles nécessaires ? En quoi peuvent-elles être pernicieuses ? Sur des exemples liés à l'histoire, à l'enseignement, et au mouvement contemporain des mathématiques, je m'efforcerai de montrer les définitions comme aboutissements de processus, comme commencement de théories, comme merveilles et comme pièges.
Thème
Documentation
Documents pédagogiques
Texte de la 174e conférence de l’Université de tous les savoirs donnée le 22 juin 2000.
Nécessité et pièges des définitions mathématiques
par Jean-Pierre Kahane
Cet amphithéâtre est impressionnant pour moi par sa taille, et aussi par le fait que je ne vous connais pas. Il peut être utile que je me présente à vous. Je suis mathématicien, retraité, mon domaine de compétence est l’analyse de Fourier, qui touche à l’analyse fonctionnelle, à la théorie des probabilités, et, plus ou moins, à toutes les branches des mathématiques. Comme beaucoup de mathématiciens, je suis intéressé par l’histoire des mathématiques et par leur enseignement. Ces préoccupations s’inscrivent bien dans une vision du passé et de l’avenir des sociétés humaines, oui les mathématiques me paraissent avoir un rôle important à la fois par leur permanence et par leur mouvement.
Je viens de nommer l’analyse de Fourier, l’analyse fonctionnelle, la théorie des probabilités. L’analyse de Fourier consiste à décomposer des fonctions en morceaux qu’on appelle les harmoniques, et à les reconstituer à partir de ces morceaux. L’analyse fonctionnelle consiste à traiter les fonctions comme des points dans des espaces qu’on appelle espaces fonctionnels. Les probabilités traitent de l’incertain pour aboutir à des certitudes.
Les définitions que je viens de donner n’ont d’autre utilité que d’amorcer notre entretien. Elles sont vagues et inoffensives, elles ne sont nécessaires ni à la recherche ni à l’enseignement, et à ma connaissance elles ne renferment pas de pièges.
Or, si peu que je sache de vous, je crois savoir que vous être venus pour entendre parler de la nécessité et des pièges des définitions mathématiques. Je soupçonne que vous êtes plus curieux des pièges que de la nécessité, et aussi que vous avez peut-être des questions pièges à me poser tout à l’heure, auxquelles je ne saurai pas répondre. Mon but est aussi d’attirer l’attention sur les pièges. Je compte donc vous parler tout à l’heure des définitions mathématiques comme pièges, de vous montrer des embûches et des défis, et de vous donner des exemples de mauvaises définitions, de définitions trompeuses et de définitions impossibles. Bien sûr, nous verrons apparaître des questions de vocabulaire et de logique, et peut-être, à cette occasion, une réflexion sur la nature des concepts mathématiques.
Mais, pour commencer, je dois insister sur la nécessité des définitions mathématiques, sur leur rôle essentiel dans la recherche et dans l’enseignement. Dans une théorie mathématique, les propositions s’enchaînent, et les propositions de départ sont les définitions et les axiomes, intimement mêlés. Ainsi, les définitions apparaissent au commencement de toute théorie. Je vais naturellement traiter de ce thème, les définitions comme commencement, mais je débuterai par l’aspect opposé, les définitions comme aboutissement d’un long processus de recherche.
Je vais donc vous parler des définitions comme aboutissement, puis des définitions comme commencement, puis des définitions comme pièges.
L’idée que la définition est un aboutissement ne vous est peut-être pas familière. Pour l’illustrer, je prendrai un exemple, mon exemple favori. Au niveau de la licence, on enseigne un théorème superbe, qui tient en trois mots : « L2 est complet ». Voici la signification des termes. L2 est l’espace constitué par les fonctions dont le carré est intégrable au sens de Lebesgue. On y définit des distances, des angles, toute une géométrie calquée sur la géométrie ordinaire de l’espace euclidien. Un espace est complet si on peut y manipuler les suites comme dans l’espace ordinaire : si les points d’une suite se rapprochent les uns des autres quand l’ordre des termes augmente, la suite tend vers une limite. Le fait que L2 est complet est essentiel en mathématiques et en physique. Le triomphe de l’intégrale de Lebesgue sur les autres théories de l’intégrale, c’est principalement ce théorème, et plus généralement le fait que les espaces Lp constitués des fonctions dont la p-ième puissance de la valeur absolue est intégrable au sens de Lebesgue sont, pour p³1, des espaces complets. On distingue ce théorème sous le nom de Frédéric Riesz, et il date de 1910.
Mais Frédéric Riesz ne l’a pas énoncé sous cette forme. À l’époque, il n’y a pas d’espace Lp ni d’espaces complets. Mais il y a un grand intérêt pour l’intégrale de Lebesgue et pour les séries de Fourier. En 1907, le hongrois Frédéric Riesz et l’autrichien Ernst Fischer s’affrontent à ce sujet, courtoisement mais fermement, dans les Comptes Rendus de l’Académie des sciences. Tous deux établissent une propriété très remarquable des séries de Fourier, à savoir que les formules de Fourier (d’un côté, calcul des coefficients à partir de la fonction, et de l’autre, calcul de la fonction à partir des coefficients) font passer naturellement de l’espace L2 à l’espace ℓ2 constitué par les suites de nombres dont les carrés forment une suite sommable. Plus tard, en 1949, Frédéric Riesz qualifiera ce théorème, auquel on donne les deux noms de Fischer et de Riesz, de « billet permanent aller-retour entre deux espaces à une infinité de dimensions ».
Le problème, sur lequel Riesz revient dans sa dernière note, est de caractériser les coefficients de Fourier des fonctions intégrables. On n’y parvient pas, mais on caractérise les coefficients de Fourier des fonctions de carré intégrable : c’est le « billet aller-retour » dont il parle en 1949, et que l’on appelle, selon les pays, théorème de Riesz-Fischer ou de Fischer-Riesz. La méthode de démonstration introduit l’espace que nous appelons L2 et la propriété que nous appelons : être complet. C’est cette méthode que nous retenons maintenant comme théorème, et nous utilisons les concepts sous-jacents « Lp » et « complet » comme notions parfaitement définies. Ainsi le théorème tient en trois mots, mais les deux mots « L2 » et « complet » sont l’aboutissement d’une longue démarche, un véritable élixir de pensée mathématique. La substance du problème, de la solution, de la méthode, est passée dans les définitions.
Je me suis attardé sur cet exemple mais le phénomène m’apparaît comme absolument général : les définitions pertinentes en mathématiques sont l’aboutissement d’une longue histoire et de beaux travaux. L’histoire, dans ce cas, remonte à Joseph Fourier et au-delà. Riesz et Fischer ont été inspirés par Lebesgue et par Hilbert, et leur géométrie des fonctions a rejoint la théorie des espaces abstraits, de Maurice Fréchet, qui date de 1906. Mais ce n’est qu’en 1932, avec Stefan Banach et sa théorie des opérations linéaires, que les espaces complets prennent leur nom et leur place en analyse, et Banach indique parmi les premiers exemples les espaces Lp, ainsi nommés en hommage à Lebesgue.
La définition des espaces Lp et celle des espaces métriques complets est sans doute l’apport le plus considérable de l’analyse de Fourier à l’analyse fonctionnelle. Mais l’interaction entre les deux domaines s’est poursuivie tout au long du siècle, et elle est ponctuée par une série de définitions : outre les espaces de Hilbert et les espaces de Banach, toute une série d’espaces fonctionnels – espaces de Sobolev, espaces de Besov, espace de Schwartz, algèbre de Wiener, algèbre de Beurling, des notions très générales comme la convolution, et des outils comme la décomposition de Littlewood-Paley, les atomes et les molécules qui ont occupé l’attention au cours des années 70 et enfin les ondelettes. Je reviendrai sur la convolution et les ondelettes. Dans tous les cas que je viens de dire, les définitions sont le résultat d’un long processus, elles signifient que des notions importantes, simples et puissantes, ont été extraites du magma de connaissances qu’apporte sans cesse le mouvement des mathématiques. Une fois extraites, elles vont structurer le magma, on pourra oublier qu’elles sont un aboutissement et les prendre pour point de départ. Mais leur beauté et leur puissance viennent de ce qu’elles sont un élixir de pensée.
Il en est ainsi, je crois, des objets les plus classiques de la géométrie, les cercles et les sphères, comme des objets les plus généraux dégagés au cours du siècle : les groupes, les espaces métriques, les probabilités. Fréquemment le mot cristallise une notion. Ainsi le mouvement brownien, observé par un botaniste en 1830 , étudié par des physiciens, élaboré par Einstein et Wiener, est devenu une entité mathématique bien définie ; quand des physiciens parlent aujourd’hui du mouvement brownien, ils se réfèrent au mouvement brownien défini en mathématique, et non plus en général au mouvement que l’on peut observer de particules en suspension dans un liquide. Ainsi, dans un tout autre domaine, logique et théorie des nombres, la définition des ensembles diophantiens, qui est simple et aurait pu être donnée depuis des siècles, n’est apparue qu’en 1950, pour permettre de traduire sous la forme d’une hypothèse très générale une foule de problèmes particuliers ; l’hypothèse a été démontrée, en 1970, par le russe Matyassévitch, résolvant du même coup le dixième problème de Hilbert, et elle a valu à son auteur la médaille Fields ; aujourd’hui ces problèmes n’ont plus qu’un intérêt historique, mais les ensembles diophantiens demeurent comme objet d’étude important ; l’une des perles de la théorie est que l’ensemble des nombres premiers est diophantien, et plus précisément qu’il coïncide avec l’ensemble des valeurs prises par un certain polynôme à plusieurs variables lorsque l’on donne aux variables des valeurs entières.
Dans tous les traités de mathématiques, d’Euclide à Bourbaki et au-delà, on part des définitions. On réécrit donc l’histoire à l’envers. Cela n’est pas propre aux mathématiques : que ce soit en astronomie ou en biologie, l’exposé d’un sujet prend régulièrement pour point de départ ce qui est un aboutissement historique. On appelle cela la transposition didactique.
Le traité de Banach sur les opérations linéaires, dont j’ai déjà parlé, est un parfait exemple. Il définit tour à tour les espaces métriques (qu’il appelle « espaces D », D pour distance, ce sont les espaces où l’on définit les distances entre points), les suites de Cauchy (que, suivant Fischer, il appelle « suites convergentes »), les espaces métriques complets et la propriété de Baire (toute intersection dénombrable d’ouverts denses est dense – ce qui, maintenant, sert de définition aux espaces de Baire), les espaces de Banach qu’il appelle « espaces de type B », et, comme exemples, les espaces Lp. Comme on le voit, la terminologie s’est modifiée légèrement depuis lors, mais nous n’avons aucune peine à reconnaître nos espaces métriques, nos suites de Cauchy, nos espaces de Banach parce que les définitions sont parfaitement formalisées. Le fait que les espaces Lp sont des espaces de Banach est le théorème de Riesz que j’ai raconté. Très vite, les définitions prennent chair. Les contemporains pouvaient y reconnaître, merveilleusement agencées, des connaissances éparses élaborées par les analystes et les topologues dans le large domaine que les mathématiciens polonais de l’entre-deux-guerres appelaient théorie des ensembles. Pour nous, aujourd’hui, ces notions sont à la fois classiques et très actuelles. La propriété de Baire n’a cessé de produire des merveilles en analyse ; c’est l’un de nos outils conceptuels les plus puissants pour produire ou pour apprivoiser des monstres. La géométrie des espaces de Banach est un grand sujet d’étude, où les contributions françaises ont été marquantes. Les définitions données par Banach sont le point de départ non seulement de l’œuvre magistrale que constitue son livre, mais d’une grande partie de l’analyse fonctionnelle contemporaine.
J’ai évoqué Euclide, et je voudrais vous parler d’objets mathématiques familiers, le cercle et la sphère. Vous connaissez la définition du cercle selon Euclide, à partir du centre et du rayon. Elle correspond à une expérience familière, la tracé d’un cercle à l’aide d’un compas, ou d’un piquet et d’une corde. Elle est excellente comme point de départ de la géométrie du cercle, telle qu’Euclide l’expose. De fait, la géométrie plane d’Euclide est un mariage de la géométrie du triangle et de celle du cercle, et c’est par elle que la définition du cercle prend sa valeur. On pourrait définir le cercle d’autre façon. Par exemple, le cercle de diamètre AB est le lieu des points d’où l’on voit le segment AB sous un angle droit. Ou encore, le cercle est une courbe fermée de courbure constante – c’est ce qui permet à un aveugle de reconnaître qu’une assiette est circulaire en passant son doigt sur son bord. Ou encore, le cercle enferme la surface maxima pour un périmètre donné – c’est ce qui explique beaucoup de formes circulaires, comme celle de la ronde que forment des enfants en se tenant par la main. Dans toutes ces définitions, il n’est plus question de centre et de rayon et effectivement, dans la vie courante, nous n’avons pas besoin du centre pour reconnaître un cercle. La force de la définition d’Euclide, c’est d’abord que tout le monde peut la comprendre, et ensuite qu’elle permet, par des enchaînements plus ou moins laborieux, de retrouver ces définitions possibles, et bien d’autres, comme propriétés caractéristiques du cercle. Les propriétés angulaires se trouvent déjà chez Euclide, mais il a fallu attendre Newton pour la courbure , et la fin du XIXe siècle pour la propriété isopérimétrique.
Le cercle est un objet inépuisable, et il a pris de nouveaux visages au cours du XXe siècle. Au départ, c’est un objet de la géométrie euclidienne, la géométrie dont les invariants sont les distances et les angles. Mais les mathématiques progressent, comme les êtres vivants, par perte de structure. En perdant comme invariants les distances et les angles mais en conservant les rapports de distances entre points lignés, on obtient la géométrie affine, et le cercle est le paradigme de l’ellipse. En ne gardant que des rapports de rapports, des birapports, on obtient la géométrie projective, et le cercle est alors le modèle de la conique. En conservant seulement la structure topologique du plan, le cercle apparaît comme l’archétype de la courbe fermée plane la plus générale, la courbe de Jordan. On peut aussi oublier que le cercle est une figure plane, et le considérer comme un objet topologique sur lequel opèrent des rotations. Dans la littérature contemporaine, lorsque l’on parle du cercle, c’est ordinairement de cet objet topologique qu’il est question. L’étude des systèmes dynamiques, où les français se sont particulièrement distingués, d’Henri Poincaré à Jean-Christophe Yoccoz, débute avec la considération de transformations du cercle en lui-même que l’on itère, et de l’allure des orbites d’un point, c’est-à-dire des images successives de ce point au cours des transformations itérées. Tous les phénomènes périodiques peuvent se représenter sur le cercle, et les séries de Fourier peuvent être considérées comme une étude approfondie du cercle considéré comme groupe topologique. Quand il y a plusieurs périodes, le cercle doit être remplacé par un tore, de sorte que, bizarrement, en analyse de Fourier, le cercle apparaît comme un tore à une dimension, et on le désigne non par C, qui est la lettre réservée au corps des nombres complexes, mais par T. On peut passer sa vie – c’est mon cas – à regarder ce qui se passe sur le cercle T.
Il en est à peu près de même pour la sphère. Il est légitime, comme le fait Euclide, de la définir au moyen du centre et du rayon ; c’est là le bon point de départ. Mais cela ne correspond plus à une expérience familière. Pour les Grecs du temps de Platon, l’expérience familière est celle des balles à douze pièces multicolores qu’évoque Socrate dans Phédon et qui sont pour lui comme une représentation de la Terre vue du ciel. Platon explique d’ailleurs dans Timée que c’est bien là le dodécaèdre régulier, le laissé pour compte des polyèdres réguliers qui représentent les quatre éléments, qui a servi au Dieu pour façonner l’univers. La sphère, pour Platon, est la figure la plus parfaite et la plus semblable à elle-même. « La figure la plus semblable à elle-même » n’est pas une bonne définition mathématique, mais c’est une vision très riche de la sphère, que la théorie doit tenter de retrouver à partir de la définition ; d’abord parmi les figures bornées dans l’espace, son groupe d’isométries, ou encore le groupe des déplacements qui la laisse invariante, est le plus grand possible ; ensuite, chaque petit morceau permet d’en retrouver la totalité. Ainsi, pour apprécier vraiment la définition de la sphère par le centre et le rayon, il faut au moins aller jusqu’à la formule de Girard liant l’aire, les angles et la courbure d’un triangle sphérique. La formule de Girard, convenablement interprétée, vaut d’ailleurs sur n’importe quelle surface courbe, et elle peut servir à définir la courbure intrinsèque. La sphère, elle aussi, est inépuisable.
Dans sa première leçon à l’École Normale de l’an III, qui fut aussi brillante qu’éphémère, Gaspard Monge commence par définir les objets usuels de la géométrie, en particulier les cercles et les sphères. À la fin du cours, les élèves peuvent interpeller le professeur, et des sténographes notent la discussion, ce qui nous permet d’en profiter. L’élève Joseph Fourier s’adresse à Monge. Il est satisfait de la définition de la sphère, mais non de celle du cercle, qui devrait nécessiter, selon lui, celle du plan. Il propose alors sa définition du plan, comme ensemble des points équidistants de deux points donnés ; puis celle de la droite, comme ensemble des points équidistants de trois points donnés ; puis celle du cercle, comme ensemble des points situés à une distance donnée de deux points donnés. Monde lui répond : « Citoyen, la clarté avec laquelle tu viens d’exposer tes réflexions… [est] une preuve de la sagacité de ton esprit. La définition que tu viens de donner de la ligne droite est rigoureuse…Permets-moi cependant de te faire à cet égard quelques observations ». Et Monge lui dit alors qu’il faut une certaine habitude de la géométrie, et de la ligne droite, pour comprendre sa définition, et que cela n’a pas sa place au début d’un cours. À un siècle de distance, Henri Poincaré fait écho à Monge quand il écrit dans la revue l’Enseignement mathématique en 1904 : « une bonne définition, c’est celle qui est comprise par les élèves ».
Il serait d’ailleurs intéressant de replacer dans leur temps les définitions proposées par Fourier. Bonaparte allait rapporter d’Italie la théorie des constructions faites sans la règle, avec le compas seul – c’est à ce titre qu’il allait appartenir à la première classe de l’Institut, celle des sciences. Fonder la géométrie sur la notion de distance et elle seule était, à cette époque une tentative sans lendemain. Mais, reprise par Maurice Fréchet en 1906 dans le cadre des « espaces abstraits », c’est le fondement des espaces métriques. Ce que nous appelons aujourd’hui les boules dans les espaces métriques s’appelait autrefois les sphères : ce sont les ensembles de points situés à une distance d’un point (le cercle) inférieure à un nombre donné (le rayon). Fourier ne pouvait pas soupçonner le rôle que les boules dans les espaces métriques allaient jouer dans l’analyse de Fourier.
Il convient également de réfléchir à la formule de Poincaré : « Une bonne définition, c’est celle qui est comprise par les élèves ». C’est un objectif plus qu’une réalité. Plus la définition est générale et puissante, moins elle est directement assimilable. Groupes, espaces métriques, compacité, complétude, espaces vectoriels se définissent en quelques lignes, parfois en quelques mots. Mais ces définitions ne prennent sens que lorsque l’on avance assez dans la théorie pour voir au moins une partie des résultats qui, historiquement, avaient amené à élaborer ces notions. Ainsi les définitions doivent être admises, apprises, avant de pouvoir être véritablement comprises. Pour qu’elles soient admises et apprises, il faut les commenter et les justifier par des exemples et des contre-exemples. Pour qu’elles soient de mieux en mieux comprises, il faut développer les théories dont elles ne sont que le commencement.
Le premier piège des définitions concerne celles qui sont les plus achevées, les plus parfaites. C’est de croire facile à acquérir ce qui est simple à énoncer. Il me paraît lié à une certaine vision des mathématiques selon laquelle les objets mathématiques et leurs définitions préexistent à l’homme dans un monde idéal, comme des pommes à cueillir dans l’arbre de la connaissance. Une fois la pomme découverte et cueillie, pourquoi ne pas la consommer tout de suite ? Ainsi de la structure de groupe, si simple, si belle, si puissante, que l’on pouvait s’étonner de l’avoir découverte si tard, et qu’il fallait de se hâter de l’introduire à la base de l’enseignement mathématique. C’était l’époque des réformateurs des années 1960, et elle s’est traduite par un échec. Si au contraire on considère les définitions les plus simples comme l’aboutissement d’un long processus de distillations successives, comme un élixir de pensée, on doit traiter chacune comme une forte eau-de-vie, à sentir et à goûter, à consommer lentement avec, si possible, un peu d’aliment solide à côté, à digérer et à assimiler en prenant son temps.
Le second piège est de faire trop confiance aux définitions. Or il y a des définitions malvenues, inutiles ou même nuisibles. Je m’en tiendrai à un exemple, la définition des séries. Depuis un demi-siècle, à la suite de Bourbaki, les ouvrages d’enseignement et les dictionnaires donnent des séries la définition suivante : on appelle série un coupe de deux suites (un) et (sn), liées par la relation sn = u1 + u2 + … + un ; la suite (un) est celle des termes, la suite (sn) celle des sommes partielles ; on dit que la série converge et qu’elle a pour somme s lorsque la suite (sn) converge et qu’elle a s pour limite. Cette définition sonne bien, mais elle est mauvaise. Dans le couple, la seconde suite n’apporte rien, elle est complètement déterminée par la première. La définition ne se justifie que par un jeu de mots : la série converge lorsque la seconde suite converge. Sous ce seul rapport, elle est malvenue. Mais il y a pire : elle ancre d’idée que la seule chose qui importe pour une série c’est qu’elle converge ou qu’elle diverge. Or ce qu’il y a de vivant dans les séries est ailleurs : les séries multiples, pour lesquelles il n’y a aucune notion évidente de somme partielle, les procédés de sommation qui permettent de donner une somme à des séries divergentes, les séries qui convergent rapidement ou lentement, les séries qu’on ordonne selon la taille des termes, les séries asymptotiques qui sont partout divergentes et qui permettent pourtant des calculs numériques d’une grande précision. Quand Fourier puis Cauchy ont précisé ce qu’il fallait entendre par série convergente, c’était un progrès conceptuel majeur. Mais penser qu’il s’agit là de l’essence de la notion de série, c’est en ignorer complètement la richesse. Euler et Bernoulli, au XVIIIe siècle, maniaient avec dextérité des séries divergentes. Fourier, ensuite, a utilisé ses séries trigonométriques pour calculer des températures au moyen, comme il le dit, de séries « extrêmement convergentes ». Les séries de fonctions, et particulièrement les séries trigonométriques, imposent d’introduire divers procédés de sommation. Se limiter à la convergence et à la divergence, c’est châtrer la notion.
Alors, qu’est-ce qu’une série ? Pour moi, c’est une somme infinie à laquelle on s’efforce de donner un sens. Le sens peut être purement formel : sur les écritures de sommes infinies on peut faire des additions, des multiplications et bien d’autres opérations. Il y a toute une algèbre des séries formelles qui ne nécessite aucunement de donner une valeur à la somme d’une série. Cependant, le plus souvent, une série est une somme infinie à laquelle on tente de donner une valeur. Cette valeur peut être définie sans ambiguïté si les termes sont positifs ou s’ils forment une famille sommable. Sinon, tout dépendra du procédé de sommation. Dans tous les cas, le monde de calcul mérite attention. Dans tout ce que je viens de dire, il y a matière à plusieurs définitions mathématiques (séries formelles, procédés de sommation, familles sommables), mais je ne donne pas de définition mathématique de la série.
J’ajoute un mot sur les séries de Fourier. Pour Fourier, comme je l’ai dit, elles étaient d’abord un outil dans sa théorie analytique de la chaleur. Mais il en a vu la portée générale, et il en a fait un objet d’étude qui a donné lieu depuis deux siècles à des travaux difficiles et importants. Les sommes partielles des séries de Fourier ne sont pas des objets faciles à manipuler à un point de vue général. On sait, depuis plus d’un siècle (de Bois Reymond 1873) que la série de Fourier d’une fonction continue peut diverger en un point, et depuis 1926 (Kolmogorov) que la série de Fourier d’une fonction intégrable au sens de Lebesgue (c’est-à-dire une fonction de la classe L1) peut diverger partout. Ce n’est que depuis 1968 (Carleson puis Hunt) que nous savons que les séries de Fourier des fonctions des classes Lp, p>1, convergent presque partout. Pour les fonctions de la classe L1, la vitesse de divergence est encore un mystère, mais un grand progrès a été réalisé en 1999 par le mathématicien russe Koryagin. Il s’agit là de remarquables travaux d’orfèvrerie.
Cependant il y a une question plus naturelle que la convergence des sommes partielles au point de vue du calcul numérique : c’est la convergence des sommes que l’on obtient en négligeant les termes les plus petits, disons, les termes de valeur absolue plus petite qu’un ε donné, quand ε tend vers zéro. La question s’est posée dans le cadre d’espaces fonctionnels, tels que L1 ou les Lp, au début des années 1960, et j’y ai apporté les premières contributions. Elle se pose aujourd’hui, et elle a donné lieu à de beaux travaux, en ce qui concerne le comportement presque partout. Je me borne à indiquer très grossièrement les résultats : ils sont négatifs, c’est-à-dire que l’on a généralement divergence, dans le cas des séries trigonométriques, c’est-à-dire des séries de Fourier proprement dites, et positifs, c’est-à-dire que l’on a convergence, aussi bien dans les espaces fonctionnels usuels que presque partout, dans le cas des séries d’ondelettes.
Ainsi les séries de Fourier sont-elles historiquement responsables du meilleur et du pire. Le meilleur, c’est l’élaboration de la notion de convergence, les travaux magnifiques sur la convergence et la divergence, les procédés de sommation, l’introduction des espaces fonctionnels dont j’ai parlé à l’occasion du théorème de Riesz-Fischer, la théorie des séries orthogonales dont l’avatar contemporain le plus important est la théorie des ondelettes. Le pire, c’est la fixation sur la convergence, en fossilisant l’apport de Fourier et Cauchy. Et cette fixation aboutit à la définition inconvenante, que j’ai donnée tout à l’heure, de la série.
En fait, la notion de série est trop riche pour se prêter à une définition mathématique. C’est une sorte de champ mathématique à l’intérieur duquel des parcelles peuvent être clairement délimitées par des définitions mathématiques précises et pertinentes, mais qu’il ne convient pas de délimiter lui-même de cette façon. Naturellement, la mauvaise définition n’a jamais empêché les mathématiciens de travailler sur les séries comme il convenait. Le piège, il est pour ceux qui enseignent et qui apprennent les mathématiques.
La situation est voisine pour l’intégrale. Dans les programmes de lycée en vigueur l’an dernier, on définissait l’intégrale d’une fonction sur un intervalle comme la différence des valeurs de sa primitive aux extrémités de l’intervalle. On prenait donc comme définition la formule ∫abf(x)dx = F(b) – F(a) que l’on appelle, dans d’autres présentations, le théorème fondamental du calcul intégral. On partait donc de l’intégration comme opération inverse de la dérivation, on partait de l’équation différentielle y’ = f(x) dont l’intégrale, au sens des équations différentielles, s’appelle la primitive de f. Cette définition n’est pas absurde : elle inscrit l’intégrale dans le cadre de la théorie des équations différentielles, elle se prête d’emblée au calcul formel, issu de Laplace et Lionville, auquel les ordinateurs donnent une nouvelle jeunesse, et elle correspond à une expérience courante, celle des compteurs kilométriques des voitures qui mesurent des distances en intégrant des vitesses. Partir des équations différentielles et introduire de cette façon les fonctions usuelles comme le logarithme et l’exponentielle, et même les fonctions trigonométriques, et traiter l’intégrale comme un aspect du calcul formel est donc un choix possible.
Le piège, c’est qu’il entraîne vers les aspects les plus formels du calcul intégral, vers les exercices de calcul, au détriment de la compréhension de ce qu’est l’intégrale. Alors, qu’est-ce que l’intégrale ? C’est une question qui a intéressé les mathématiciens au cours du XIXe siècle, en relation encore une fois avec l’analyse de Fourier, pour donner un sens à l’intégrale qui figure dans les formules donnant les coefficients de Fourier. Cauchy s’y est attaqué, puis Riemann, et l’intégrale de Riemann est apparue pendant quelques dizaines d’années comme l’essence même de la notion. Puis Lebesgue a proposé sa définition, dont nous avons vu les avantages sous la forme du théorème de Riesz-Fischer. Le XXe siècle a connu une explosion des théories de l’intégration, avec Denjoy et le calcul des primitives, Daniell et les intégrales fonctionnelles, Wiener et la théorie du mouvement brownien, Kolmogorov avec ses espaces de probabilités, Schwartz avec ses distributions, Itô avec ses intégrales stochastiques, Feynman avec ses intégrales de chemins, dont Pierre Cartier et Cécile de Witt ont donné récemment une vraie définition mathématique. Qu’est-ce qu’il y a de commun à toutes ces intégrales ? C’est ce que Youri Menin appelle le point de vue du physicien : l’intégrale, c’est la quantité de quelque chose dans un domaine. Ce n’est pas une définition mathématique, mais c’est la vision qui permet de saisir la portée de la notion ; par exemple, l’intégrale peut représenter une aire, un volume, un flux, une énergie, etc. Cela a une conséquence pédagogique : dans les programmes des lycées, lorsqu’on aborde l’intégrale, il vaut mieux partir du calcul des aires que du calcul des primitives. C’est l’introduction naturelle aux méthodes d’intégration approchée et à l’aspect numérique de l’intégration.
Le piège, en tout cas, serait de croire qu’il existe une et une seule définition correcte de l’intégrale. Il faut aller loin en analyse, en géométrie, en probabilités, pour que les divers aspects de l’intégrale se rejoignent. C’est un champ encore bien plus vaste et plus riche que celui des séries. Il faut prendre la définition comme une porte d’entrée et non comme une délimitation du champ.
Ce que je viens de dire des séries et des intégrales vaut pour un grand nombre de sujets. Je vais me borner comme exemples aux convolutions, aux ondelettes et aux fractales.
Le terme convolution est apparu au cours de ce demi-siècle, mais la notion était bien connue des physiciens : l’action d’un appareil sur un signal est une convolution, et la recherche du signal à partir de l’observation est la déconvolution. Cela s’écrit A*X = B : A est la fonction d’appareil, X le signal inconnu, * le symbole de la convolution, B ce que l’on observe. La théorie de la convolution est multiforme : on la trouve en analyse de Fourier avec Norbert Wiener, en théorie des distributions avec Laurent Schwartz, et à chaque pas en analyse numérique et en probabilités. Mais je ne connais aucune définition mathématique qui couvre tous les cas.
Yves Meyer[1] a parlé ici même des ondelettes, et il n’en a donné une définition, avec réticence, qu’en réponse à une question. C’est que le champ occupé par les ondelettes dépasse maintenant de beaucoup toutes les définitions possibles. La situation a considérablement évolué depuis septembre 1985 et la première conférence qu’il a donnée sur le sujet, au Collège de France. Yves Meyer venait de trouver une étrange fonction, qui partageait beaucoup de propriétés avec la fonction en escalier de Haar qui vaut 1 entre 0 et 1/2, -1 entre 1/2 et 1, et 0 ailleurs, mais qui était très régulière : il l’avait définie, elle était déjà tabulée et utilisée, c’était l’ondelette de Meyer, elle apparaissait déjà comme aussi légitime et immuable que les sinus et les cosinus. Or, dans les années qui ont suivi, les ondelettes ont poussé comme des champignons, avec des ondelettes de diverses régularités et diverses formes, adaptées à différents usages. L’essentiel est qu’il y a des systèmes orthogonaux d’ondelettes analogues au système de Haar, et des séries d’ondelettes analogues aux séries de Haar. Mais cela même est une délimitation trop étroite. Yves Meyer a évité le piège en donnant une vue du champ mathématique des ondelettes de l’extérieur, par l’histoire et les applications.
La situation est encore plus évidente pour les fractales. Lorsque son premier livre est apparu, il y a plus de vingt ans, sous le titre Les objets fractals, on avait cru piéger Benoît Mandelbrot en le sommant de donner une définition des fractales. Il n’avait pas réussi à donner de bonne définition, et il n’y en pas. Les fractales sont les objets de la géométrie fractale comme les figures sont les objets de la géométrie. On peut en donner une vision par des exemples et des commentaires, mais il serait imprudent de délimiter le champ de manière précise. Par contre, à l’intérieur du champ, on peut donner des définitions précises.
C’est ainsi que certains objets, parfaitement définis, sont devenus très populaires. L’escalier du diable n’est pas autre chose que ce que Salem et moi appelions la fonction de Lebesgue construite sur l’ensemble triadique de Cantor. Il n’y a pas de doute que la nouvelle terminologie est plus parlante que l’ancienne.
Je vais conclure en évoquant le choix des termes. En mathématiques, nous héritons non seulement de théories et de méthodes, mais de toute une terminologie que nous devons accepter. Il n’est pas question, dans un souci de cohérence, de remplacer triangle et quadrilatère par trigone et tétragone, pour s’aligner sur polygone. Il y a une certaine incohérence du langage, et elle n’a pas que des inconvénients.
Les mots ont des colorations diverses, qui contribuent à faire le paysage mathématique. Ils sont plus ou moins adaptés aux notions, plus ou moins évocateurs. « Convolution » n’est pas mauvais, « ondelette » est bon, « fractale » très bon, « l’escalier du diable » excellent. Bourbaki et Benoît Mandelbrot attestent, de manière différente, que les mathématiques contemporaines ont le souci du vocabulaire et de la langue mathématique.
Il y a, dans le choix des termes, des modes et des tendances. Par exemple, le XIXe siècle est le siècle des mots grecs, réservés aux initiés : holomorphie, monodromie, homographie, homologie, homomorphisme, homéomorphisme, homotopie, anallagmatique, etc. Ce sont des termes assez repoussants, et qui n’ont de valeur que par leur définition et l’usage que l’on en fait.
Au début du XXe siècle apparaissent des notions nouvelles et parfois révolutionnaires , et le vocabulaire semble traduire la volonté de ne pas effaroucher les anciens. C’est une explosion de « presque » et de « quasi » : le « presque partout » de Lebesgue, la « quasi-analyticité » d’Hadamard et de Borel, les fonctions « quasi-périodiques » de Bohl et Esclangon, les fonctions « presque-périodiques » d’Harold Bohr, etc.
Bourbaki est un modèle de langue, sobre et claire. Comme créateur de vocabulaire, tantôt il donne un sens mathématique précis à des mots français du langage courant, comme voisinages, filtres, compact, tantôt il forge des néologismes simples à partir du latin : injectif, surjectif, bijectif.
Le vocabulaire contemporain, au contraire de celui du début du siècle, semble accuser la rupture avec le passé – même lorsqu’il en hérite directement. Ce sont les relations d’incertitude, les fonctions non différentielles, l’analyse non linéaire, l’aléatoire, les catastrophes, le chaos. Curieusement, toutes ces notions ont des définitions mathématiques précises, mais elles entraînent l’imagination du public non prévenu vers des abîmes sans fond. Inutile d’insister sur la résonance entre ce vocabulaire et le désarroi social de notre fin de siècle.
Le début de cette conférence a dû vous donner l’impression que les mathématiques se développaient selon leur logique propre, en créant des notions quand elles étaient mûres, en les développant indéfiniment lorsqu’elles étaient pertinentes. La seule relation à la société que j’y évoquais était la communication et l’enseignement. Le dernier piège que je veux évoquer, c’est de croire les mathématiques détachées de la réalité sociale. Le simple examen de leur vocabulaire montre que ce n’est pas le cas. Et d’ailleurs, toutes les conférences de ce cycle sur les mathématiques, et toutes les manifestations qui ponctuent en France et dans le monde l’année mathématique 2000, montrent que les mathématiques sont enracinées et omniprésentes dans la réalité sociale, et qu’il est temps, selon l’un des mots d’ordre de l’année 2000, de les « faire sortir de leur invisibilité ».
[1] Voir le texte de la 170e conférence de l’Université de tous les savoirs donnée le 18 juin 2000 par Yves Meyer précédemment dans ce volume.
Dans la même collection
-
Mathématiques du monde quantique
ConnesAlainMon intention est d'expliquer d'abord comment la notion d'espace géométrique a évolué à travers la géométrie non-euclidienne, la géométrie riemannienne qui est la pierre angulaire de la relativité
-
L'anneau fractal de l'art à l'art à travers la géométrie, la finance et les sciences
MandelbrotBenoît B.Un bipède sans plumes ne devient homme qu'après avoir conquis le feu et les condiments et avoir décoré son corps, sa demeure et son temple. Au cours des millénaires, ses motifs décoratifs s'affinent.
-
Espaces courbes
BourguignonJean-PierreLa notion d'espace (intrinsèquement) courbe a mis beaucoup de temps avant de s'imposer. Pour la définir il convient de dépasser le premier modèle de géométrie systématiquement développée qu'est la
-
Les probabilités et le mouvement brownien
BianePhilippe"Le hasard est soumis à des lois, que le calcul des probabilités étudie d'un point de vue mathématique. La nature de ces lois est asymptotique, on ne peut rien déduire de la réalisation d'un événement
-
La turbulence
FrischUrielCinq siècles après les travaux de Léonard de Vinci sur le contrôle des tourbillons et de leur effet dans la rivière Arno, le sujet n'est toujours pas clos. Au XXème siècle ce sont d'abord les
-
Les nombres et l'écriture
RitterJimLa relation entre les nombres et l'écriture a été durable et féconde. Au cours de l'histoire, dans différentes cultures - dans l'Europe moderne ou contemporaine, en Chine ancienne, dans le monde arabe
-
Économie et mathématiques
EkelandIvarL' usage de la modélisation mathématique en économie, et plus généralement dans les sciences sociales, choque encore un public pourtant habitué au succès de cette modélisation dans les sciences
-
Mathématiques, modélisation et simulation
LionsPierre-LouisQue sont les simulations numériques et à quoi servent-elles ? Il s'agit de problèmes de mathématique appliquée dans lesquels on essaie de résoudre numériquement des modèles d'origine physique,
-
Espace et nombre
TitsJacques"Le thème assigné à cette conférence par le plan d'ensemble du cycle est ""Géométrie et Algèbre"" : il s'agit, comme chacun sait, de deux grands domaines des mathématiques à la fois très anciens, et
-
Théorie des noeuds
Bayer-FluckigerEvaLe but de cette conférence est de présenter l'évolution d'une discipline mathématique, la théorie des noeuds, depuis le milieu du XIXe siècle jusqu'à nos jours. À travers l'exemple de la théorie des
-
Les fondements des mathématiques
GirardJean-Yves"La "" crise des fondements "" s'ouvre en 1897 avec le paradoxe de Burali-Forti, une contradiction dans la toute jeune théorie des Ensembles. Parmi les solutions proposées, le "" Programme de Hilbert
-
Les ondelettes et la révolution numérique
MeyerYves"La "" révolution numérique "" change profondément notre vie, puisqu'elle modifie notre relation au monde et notre relation aux autres. Elle comprend le téléphone digital, le fax et la télévision
Sur le même thème
-
Tuan Ta Pesao : écritures de sable et de ficelle à l'Ile d'Ambrym
VandendriesscheEricCe film se déroule au Nord de l’île d’Ambrym, dans l’archipel de Vanuatu, en Mélanésie...
-
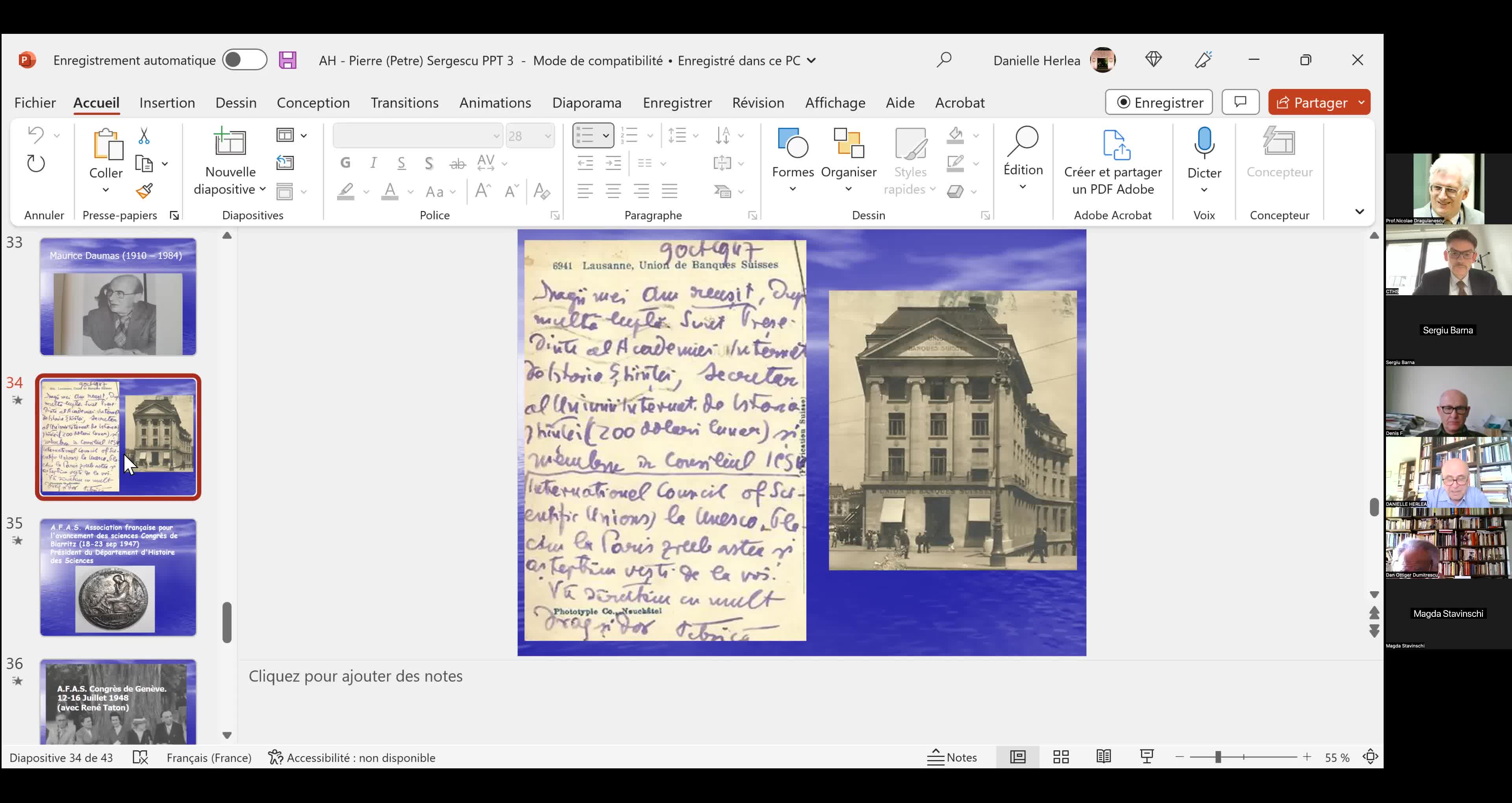
"Le mathématicien Petre (Pierre) Sergescu, historien des sciences, personnalité du XXe siècle"
HerléaAlexandreAlexandre HERLEA est membre de la section « Sciences, histoire des sciences et des techniques et archéologie industrielle » du CTHS. Professeur émérite des universités, membre effectif de l'Académie
-
Webinaire sur la rédaction des PGD
LouvetViolaineRédaction des Plans de Gestion de Données (PGD) sous l’angle des besoins de la communauté mathématique.
-
Alexandre Booms : « Usage de matériel pédagogique adapté en géométrie : une transposition à interro…
« Usage de matériel pédagogique adapté en géométrie : une transposition à interroger ». Alexandre Booms, doctorant (Université de Reims Champagne-Ardenne - Cérep UR 4692)
-
M. Lesourd - Positive Scalar Curvature on Noncompact Manifolds and the Positive Mass Theorem
LesourdMartinThe study of positive scalar curvature on noncompact manifolds has seen significant progress in the last few years. A major role has been played by Gromov's results and conjectures, and in
-
R. Perales - Recent Intrinsic Flat Convergence Theorems
PeralesRaquelThéorèmes récents de convergence plane intrinsèque
-
J. Fine - Knots, minimal surfaces and J-holomorphic curves
FineJoëlI will describe work in progress, parts of which are joint with Marcelo Alves. Let L be a knot or link in the 3-sphere. I will explain how one can count minimal surfaces in hyperbolic 4-space
-
P. Burkhardt - Pointwise lower scalar curvature bounds for C0 metrics via regularizing Ricci flow
Burkhardt-GuimPaulaWe propose a class of local definitions of weak lower scalar curvature bounds that is well defined for C0 metrics. We show the following: that our definitions are stable under greater-than-second
-
D. Semola - Boundary regularity and stability under lower Ricci bounds
SemolaDanieleThe theory of non smooth spaces with lower Ricci Curvature bounds has undergone huge developments in the last thirty years. On the one hand the impetus came from Gromov’s precompactness theorem
-
D. Stern - Harmonic map methods in spectral geometry
SternDanielOver the last fifty years, the problem of finding sharp upper bounds for area-normalized Laplacian eigenvalues on closed surfaces has attracted the attention of many geometers, due in part to
-
Y. Lai - A family of 3d steady gradient Ricci solitons that are flying wings
LaiYiWe find a family of 3d steady gradient Ricci solitons that are flying wings. This verifies a conjecture by Hamilton. For a 3d flying wing, we show that the scalar curvature does not vanish at
-
R. Bamler - Compactness and partial regularity theory of Ricci flows in higher dimensions
BamlerRichard H.We present a new compactness theory of Ricci flows. This theory states that any sequence of Ricci flows that is pointed in an appropriate sense, subsequentially converges to a synthetic flow.