Notice
1.4. Parity Checking
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
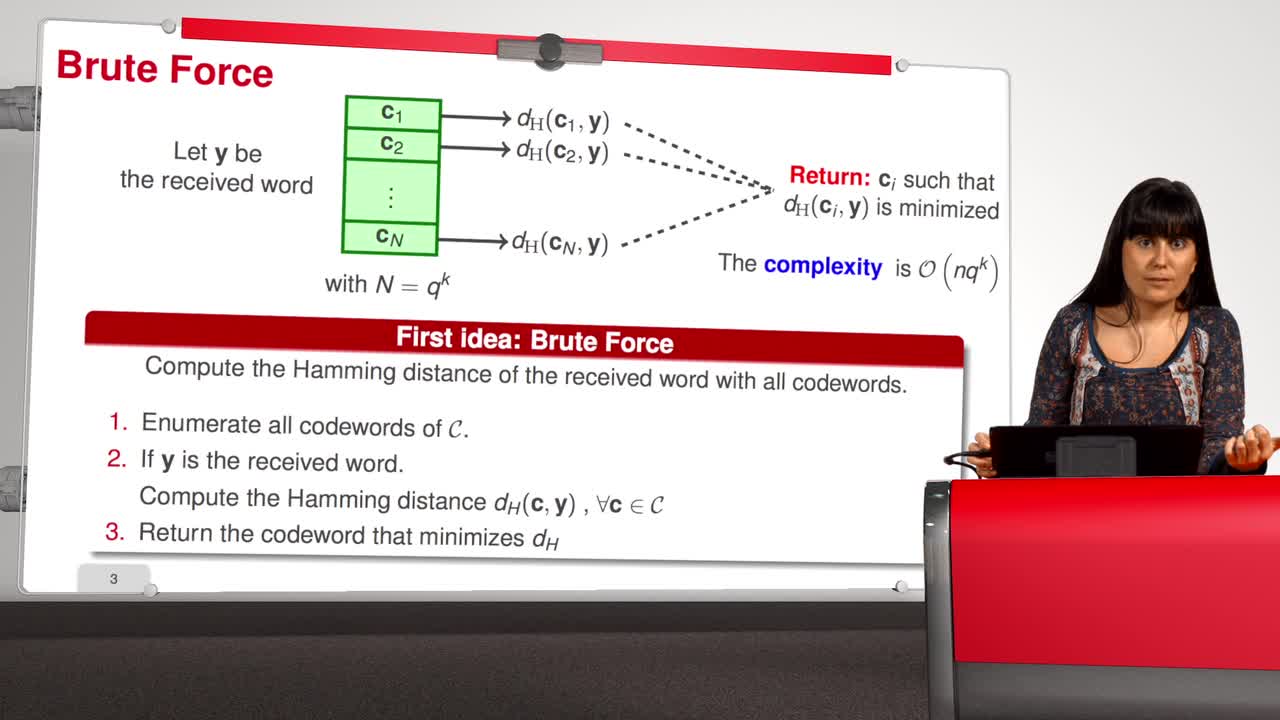
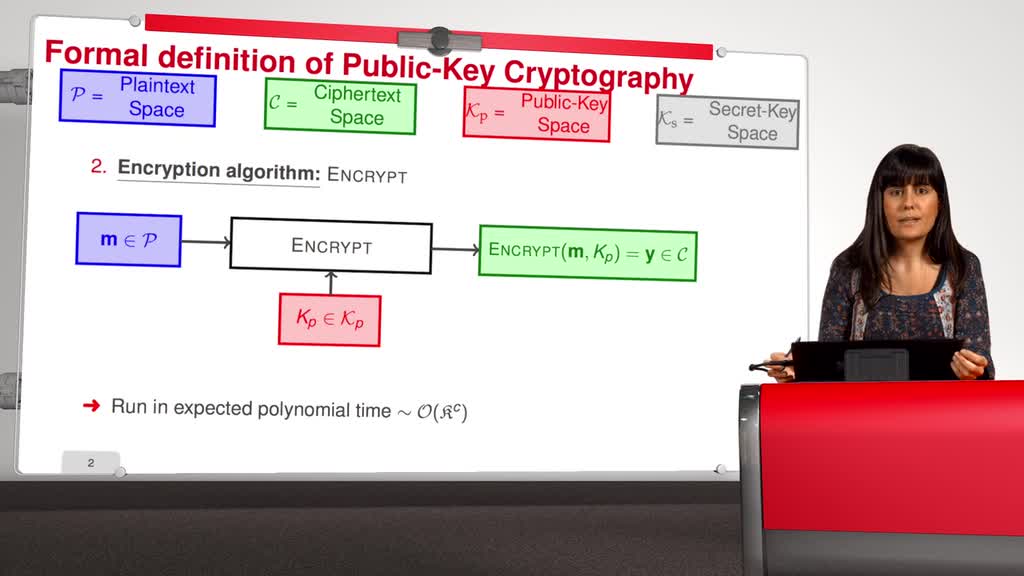
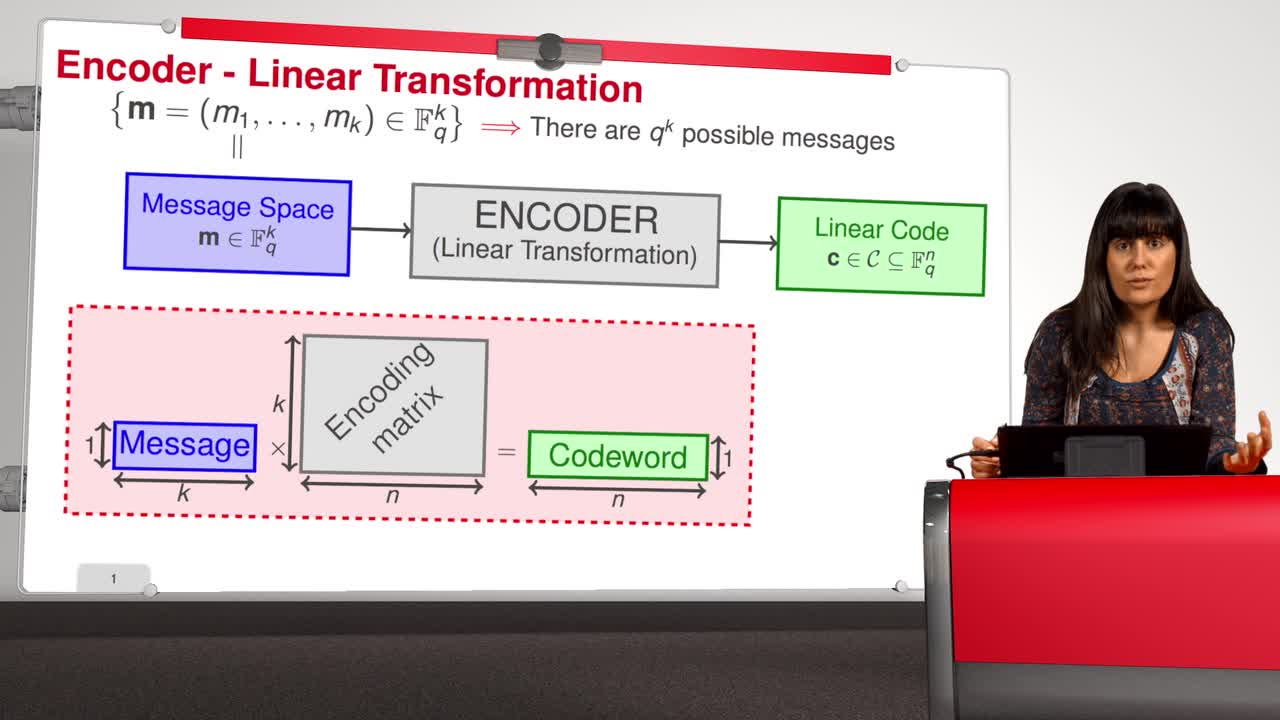
There are two standardways to describe a subspace, explicitly by giving abasis, or implicitly, by the solution space of the set ofhomogeneous linear equations. Therefore, there are twoways of describing a linear code, explicitly, as wehave seen in the previous sequence, by a generatormatrix, or implicitly, by the null space of a matrix. This iswhat we will see in this sequence. This leads to thefollowing definition: H is a parity check matrix of a linear code, ifthe code is the null space of H. In this way, any linear codeis completely specified by a
parity check matrix. Suppose that we have amessage of 4 bits, then we put them in the middle of theVenn Diagram, and we complete the empty three areasaccording to the following rules. The number of ones inevery circle is even. This gives us three redundantbits that we add to the message. We say that our circle isincorrect, if its parity is odd. So, if you modify anysymbol, then the error is propagated to the circlewhere this symbol is involved. Thus, if the circle one andthe second circle are wrong, then we deduce that an error hasoccurred in the first position. If the three circlesare wrong, then we deduce that there has been anerror in the fourth position.
Thus, the redundantinformation can be obtained from the message by means of threelinear equations or parity check.
Intervention / Responsable scientifique
Dans la même collection
-
1.2. Introduction II - Coding Theory
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we will give a brief introduction to Coding Theory. Claude Shannon's paper from 1948 entitled "A Mathematical Theory of Communication" gave birth to the disciplines of Information
-
1.6. Decoding (A Difficult Problem)
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuThe process of correcting errors and obtaining back the message is called decoding. In this sequence, we will focus on this process, the decoding. We would like that the decoder of the received
-
1.9. McEliece Cryptosystem
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuThis is the last session of the first week of this MOOC. We have already all the ingredients to talk about code-based cryptography. Recall that in 1976 Diffie and Hellman published their famous
-
1.3. Encoding (Linear Transformation)
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we will talk about the easy map of the - one-way trapdoor functions based on error-correcting codes. We suppose that the set of all messages that we wish to transmit is the set
-
1.7. Reed-Solomon Codes
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuReed-Solomon codes were introduced by Reed and Solomon in the 1960s. These codes are still used in storage device, from compact-disc player to deep-space application. And they are widely used
-
1.5. Error Correcting Capacity
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuThis sequence will be about the error-correcting capacity of a linear code. We describe the way of considering the space Fq^n as a metric space. This metric is necessary to justify the principle of
-
1.8. Goppa Codes
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we will talk about another family of codes that have an efficient decoding algorithm: the Goppa codes. One limitation of the generalized Reed-Solomon codes is the fact that the
-
1.1. Introduction I - Cryptography
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuWelcome to this MOOC which is entitled: code-based cryptography. This MOOC is divided in five weeks. The first week, we will talk about error-correcting codes and cryptography, this is an introduction
Avec les mêmes intervenants et intervenantes
-
4.7. Attack against Reed-Muller codes
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we will introduce an attack against binary Reed-Muller codes. Reed-Muller codes were introduced by Muller in 1954 and, later, Reed provided the first efficient decoding algorithm
-
5.6. An Efficient Provably Secure One-Way Function
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we are going to see how to build an efficient provably secure one-way function from coding theory. As you know, a one-way function is a function which is simple to evaluate and
-
5.1. Code-Based Digital Signatures
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuWelcome to the last week of this MOOC on code-based cryptography. This week, we will be discussing other cryptographic constructions relying on coding theory. We have seen how to do public key
-
4.5. Error-Correcting Pairs
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuWe present in this session a general decoding method for linear codes. And we will see it in an example. Let C be a generalized Reed-Solomon code of dimension k associated to the pair (c, d). Then,
-
5.4. Parallel-CFS
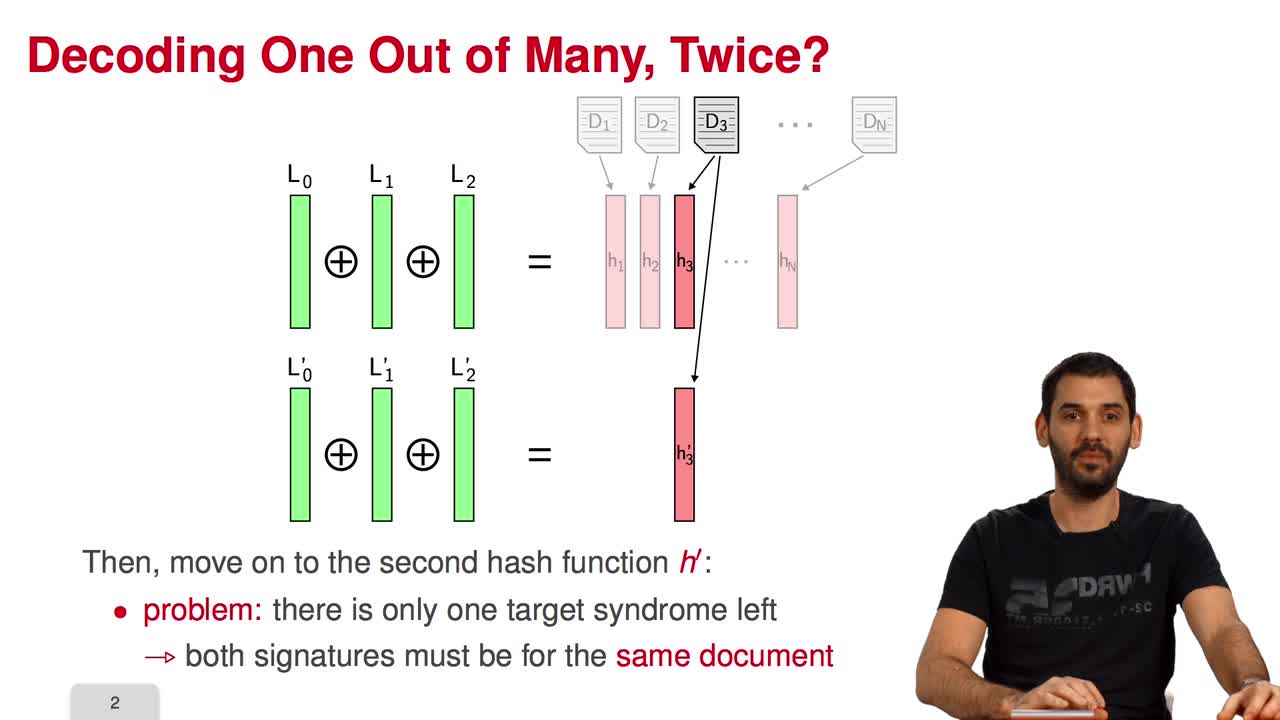
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, I will present a variant of the CFS signature scheme called parallel-CFS. We start from a simple question: what happens if you try to use two different hash functions and compute
-
4.8. Attack against Algebraic Geometry codes
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we will present an attack against Algebraic Geometry codes (AG codes). Algebraic Geometry codes is determined by a triple. First of all, an algebraic curve of genus g, then a n
-
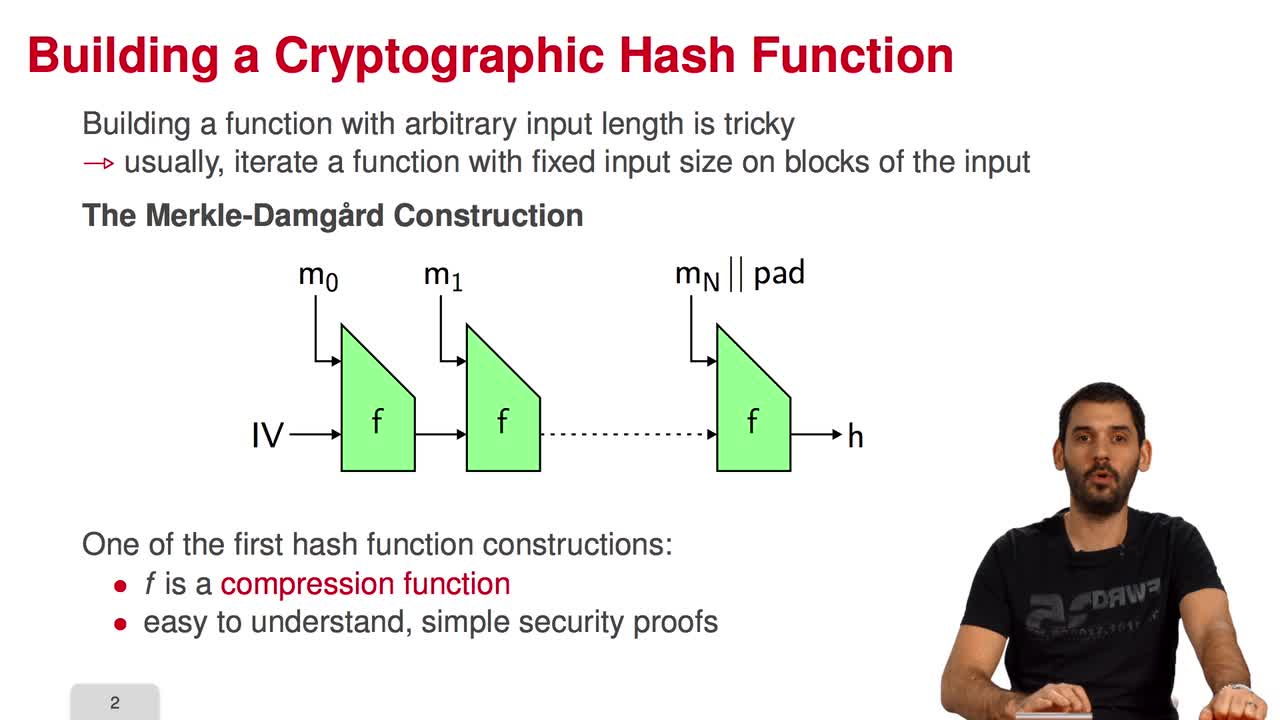
5.7. The Fast Syndrome-Based (FSB) Hash Function
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn the last session of this week, we will have a look at the FSB Hash Function which is built using the one-way function we saw in the previous session. What are the requirements for a
-
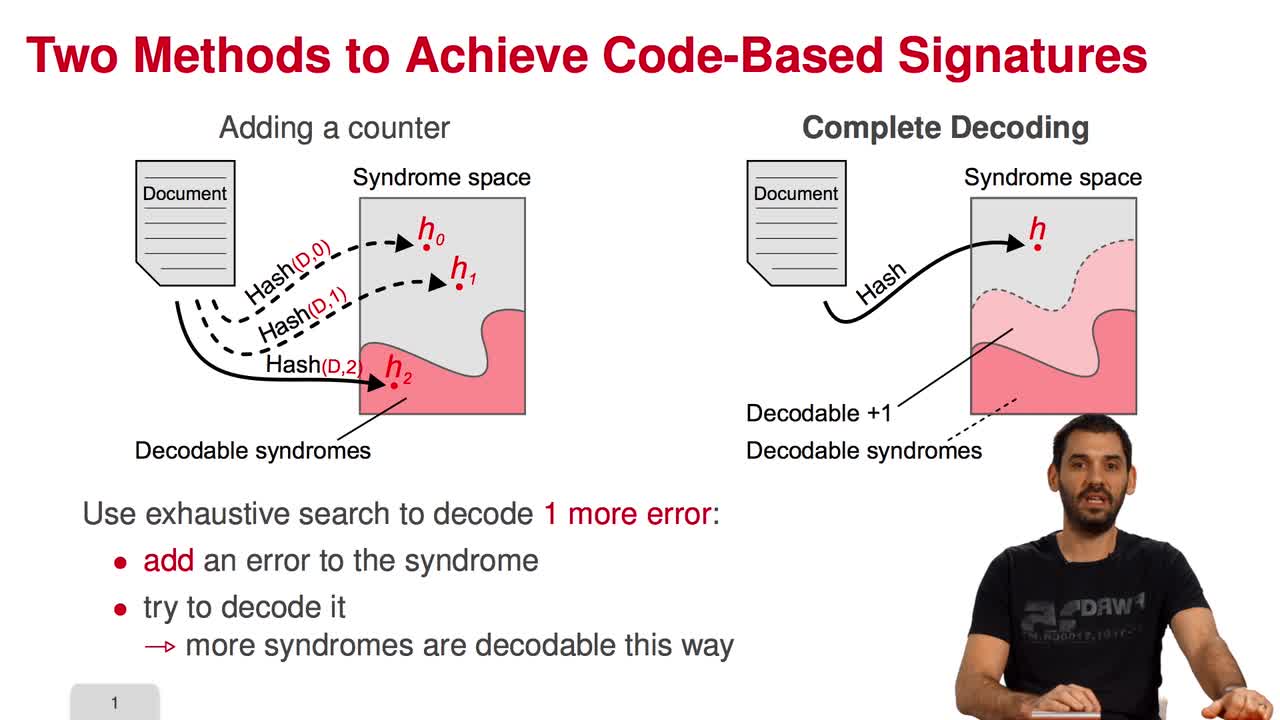
5.2. The Courtois-Finiasz-Sendrier (CFS) Construction
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, I am going to present the Courtois-Finiasz-Sendrier Construction of a code-based digital signature. In the previous session, we have seen that it is impossible to hash a document
-
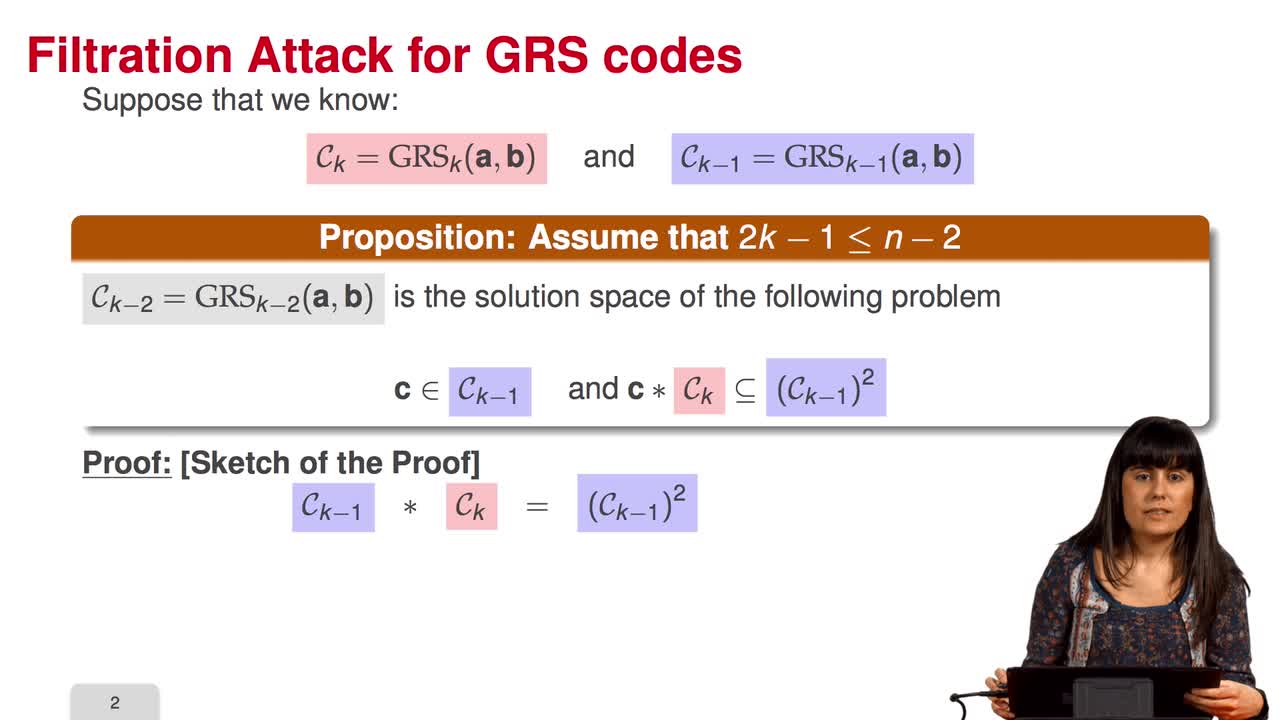
4.6. Attack against GRS codes
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session we will discuss the proposal of using generalized Reed-Solomon codes for the McEliece cryptosystem. As we have already said, generalized Reed-Solomon codes were proposed in 1986 by
-
5.5. Stern’s Zero-Knowledge Identification Scheme
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we are going to have a look at Stern’s Zero-Knowledge Identification Scheme. So, what is a Zero-Knowledge Identification Scheme? An identification scheme allows a prover to prove
-
4.9. Goppa codes still resist
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuAll the results that we have seen this week doesn't mean that code based cryptography is broken. So in this session we will see that Goppa code still resists to all these attacks. So recall that
-
4.4. Attack against subcodes of GRS codes
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we will talk about using subcodes of a Generalized Reed–Solomon code for the McEliece Cryptosystem. Recall that to avoid the attack of Sidelnikov and Shestakov, Berger and
Sur le même thème
-
Tuan Ta Pesao : écritures de sable et de ficelle à l'Ile d'Ambrym
VandendriesscheEricCe film se déroule au Nord de l’île d’Ambrym, dans l’archipel de Vanuatu, en Mélanésie...
-
Quel est le prix à payer pour la sécurité de nos données ?
MinaudBriceÀ l'ère du tout connecté, la question de la sécurité de nos données personnelles est devenue primordiale. Comment faire pour garder le contrôle de nos données ? Comment déjouer les pièges de plus en
-
Des systèmes de numération pour le calcul modulaire
BajardJean-ClaudeLe calcul modulaire est utilisé dans de nombreuses applications des mathématiques...
-
Inauguration de l'exposition - Vanessa Vitse : Nombres de Sophie Germain et codes secrets
VitseVanessaExposé de Vanessa Vitse (Institut Fourier) : Nombres de Sophie Germain et codes secrets
-
"Le mathématicien Petre (Pierre) Sergescu, historien des sciences, personnalité du XXe siècle"
HerléaAlexandreAlexandre HERLEA est membre de la section « Sciences, histoire des sciences et des techniques et archéologie industrielle » du CTHS. Professeur émérite des universités, membre effectif de l'Académie
-
Retour d'expérience sur l'utilisation croisée de plusieurs archives de fouilles
TufféryChristopheDans le cadre d'une thèse de doctorat engagée depuis 2019, une étude historiographique et épistémologique des effets des dispositifs numériques sur l'archéologie et sur les archéologues au cours des
-
Information Structures for Privacy and Fairness
PalamidessiCatusciaInformation Structures for Privacy and Fairness
-
AI and Human Decision-Making: An Interdisciplinary Perspective
CastellucciaClaudeThis seminar will talk about some of the privacy risks of these systems and will describe some recent attacks. It will also discuss why they sometimes fail to deliver. Finally, we will also show that
-
Webinaire sur la rédaction des PGD
LouvetViolaineRédaction des Plans de Gestion de Données (PGD) sous l’angle des besoins de la communauté mathématique.
-
Alexandre Booms : « Usage de matériel pédagogique adapté en géométrie : une transposition à interro…
« Usage de matériel pédagogique adapté en géométrie : une transposition à interroger ». Alexandre Booms, doctorant (Université de Reims Champagne-Ardenne - Cérep UR 4692)
-
Présentation de la rencontre. A l’heure du numérique « Quelles mesures pour la mesure ? ». Le relev…
BadieAlainTardyDominiqueMalmaryJean-JacquesZugmeyerStéphanieRencontre-Atelier de l'ANR Ornementation Architecturale des Gaules. À l’heure du numérique, « Quelles mesures pour la mesure ? ». Le relevé des blocs d’architecture décorés et l’apport des outils
-
Photogrammétrie : Performances et limitations
EgelsYvesRencontre-Atelier de l'ANR Ornementation Architecturale des Gaules. À l’heure du numérique, « Quelles mesures pour la mesure ? ». Le relevé des blocs d’architecture décorés et l’apport des outils