Notice
4.6. Si un chemin est optimal, tous ses chemins partiels sont optimaux
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
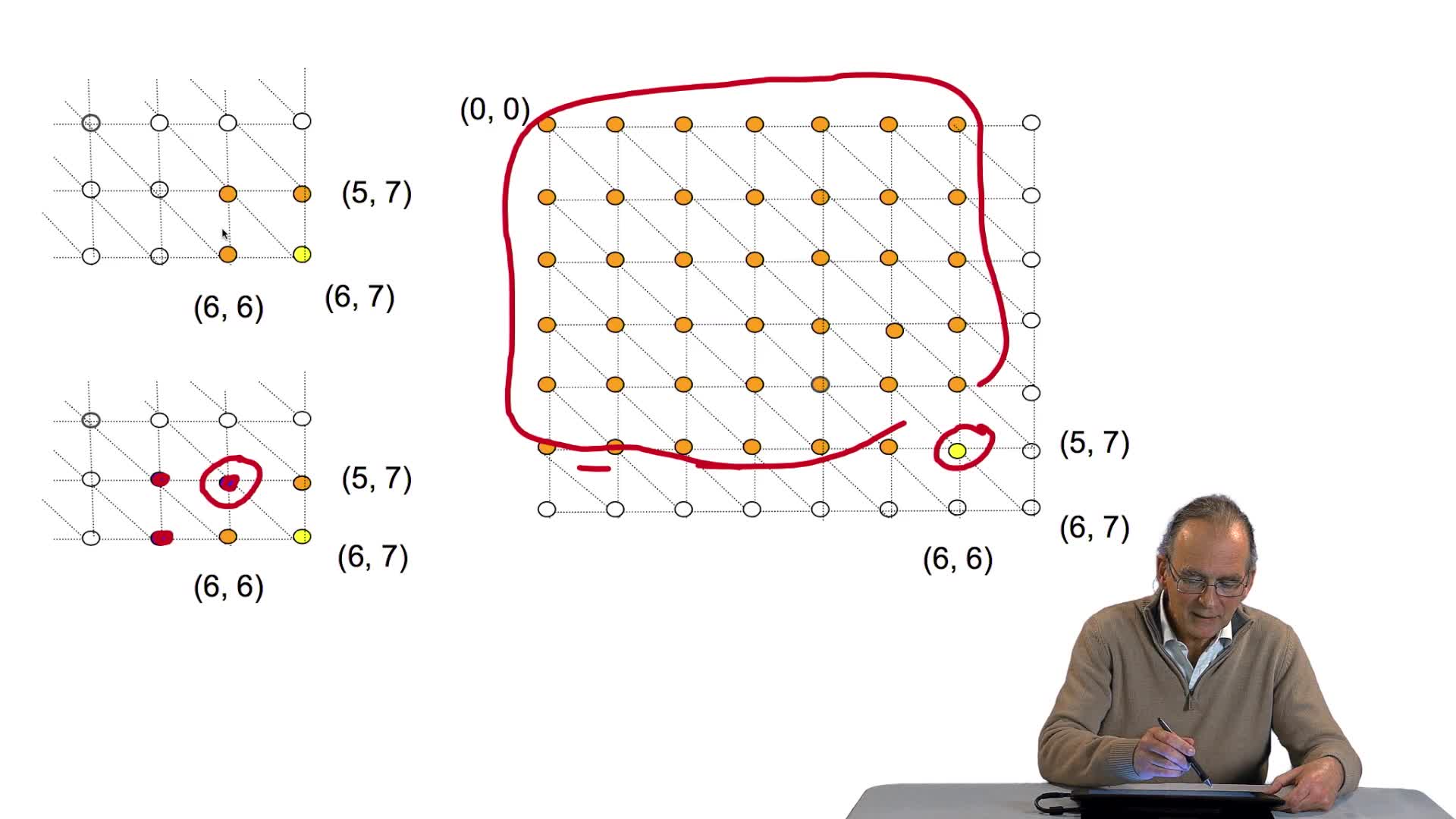
Nous cherchons à concevoir un algorithme capable de déterminer l'alignement optimal de 2 séquences. Et nous avons vu que ça revient à chercher un algorithme qui recherche un chemin optimal dans une grille. Chemin optimal, c'est-à-dire de coût de score minimal.
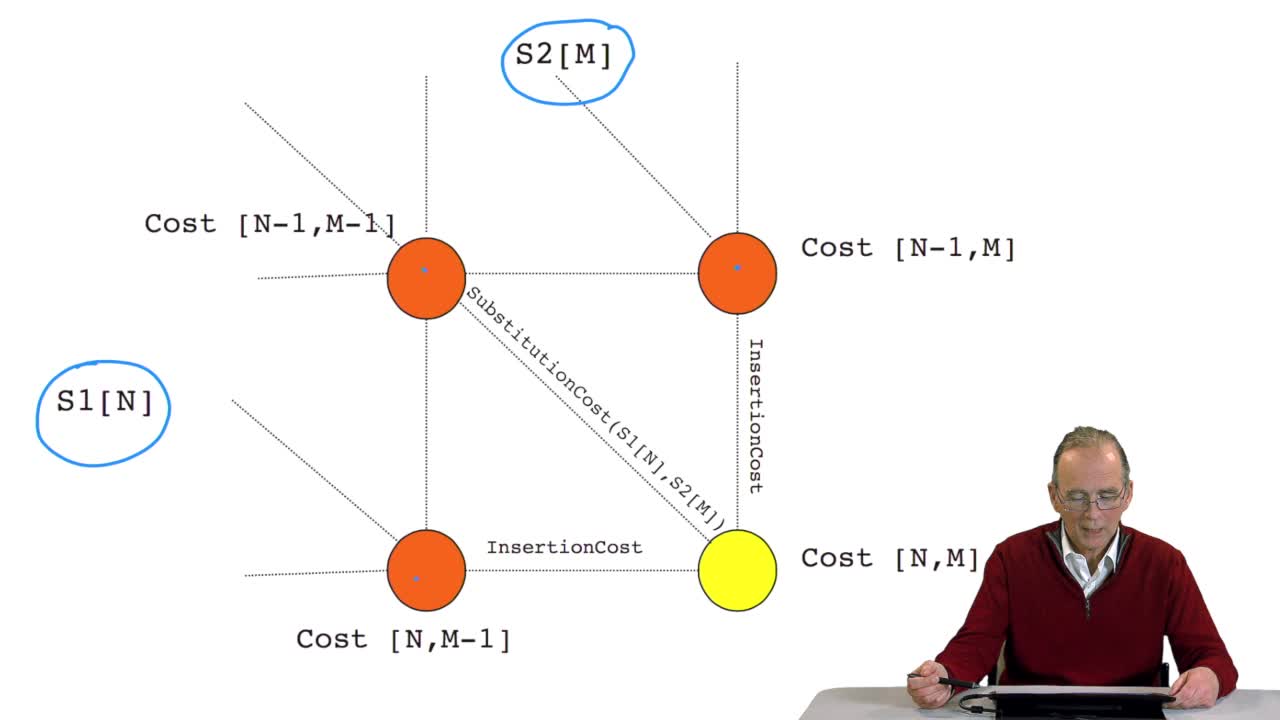
Pour bâtir cet algorithme, nous allons nous appuyer sur une propriété de ce chemin optimal qui est la suivante : si un chemin de longueur l est optimal, alors le chemin de longueur l-1 l'est aussi. Comment prouver cette propriété ? Très simplement en fait par l'absurde. C'est-à-dire qu'on va faire l'hypothèse contraire. C'est-à-dire que si le chemin de longueur L est optimal, il se peut que le chemin de longueur L-1, qu'il existe un chemin de longueur L-1 qui ne le soit pas. Et on arrivera à une contradiction. Ce qui va montrer par l'absurde, la véracité de cette affirmation-là. On voit également qu’un chemin de longueur L-1 correspond sur l'alignement à un alignement de longueur L-1 également. Correspondance, on l'avait vu, entre alignement et chemin...
Intervention
Dans la même collection
-
4.5. Un alignement de séquences vu comme un chemin dans une grille
RECHENMANN François
PARMENTELAT Thierry
Pour comparer deux séquences entre elles, il faut donc les aligner. Aligner ces deux séquences suppose faire des hypothèses d'insertion, délétion, aux bons endroits. Ça signifie, d'un point de vue
-
4.9. Éviter la récursivité : une version itérative
RECHENMANN François
PARMENTELAT Thierry
La fonction récursive que nous avons obtenue est d'un code assez compact et plutôt élégant, mais effectivement peu efficace. Pourquoi ? Rappelons son fonctionnement. Cette fonction est d'abord appelée
-
4.3. Quantifier la similarité de deux séquences
RECHENMANN François
PARMENTELAT Thierry
Le principe est donc de rechercher, dans les bases de données, des séquences similaires à celles que nous sommes en train d'étudier. Nous faisons aussi l'hypothèse que plus les séquences sont
-
4.7. Coûts et alignement
RECHENMANN François
PARMENTELAT Thierry
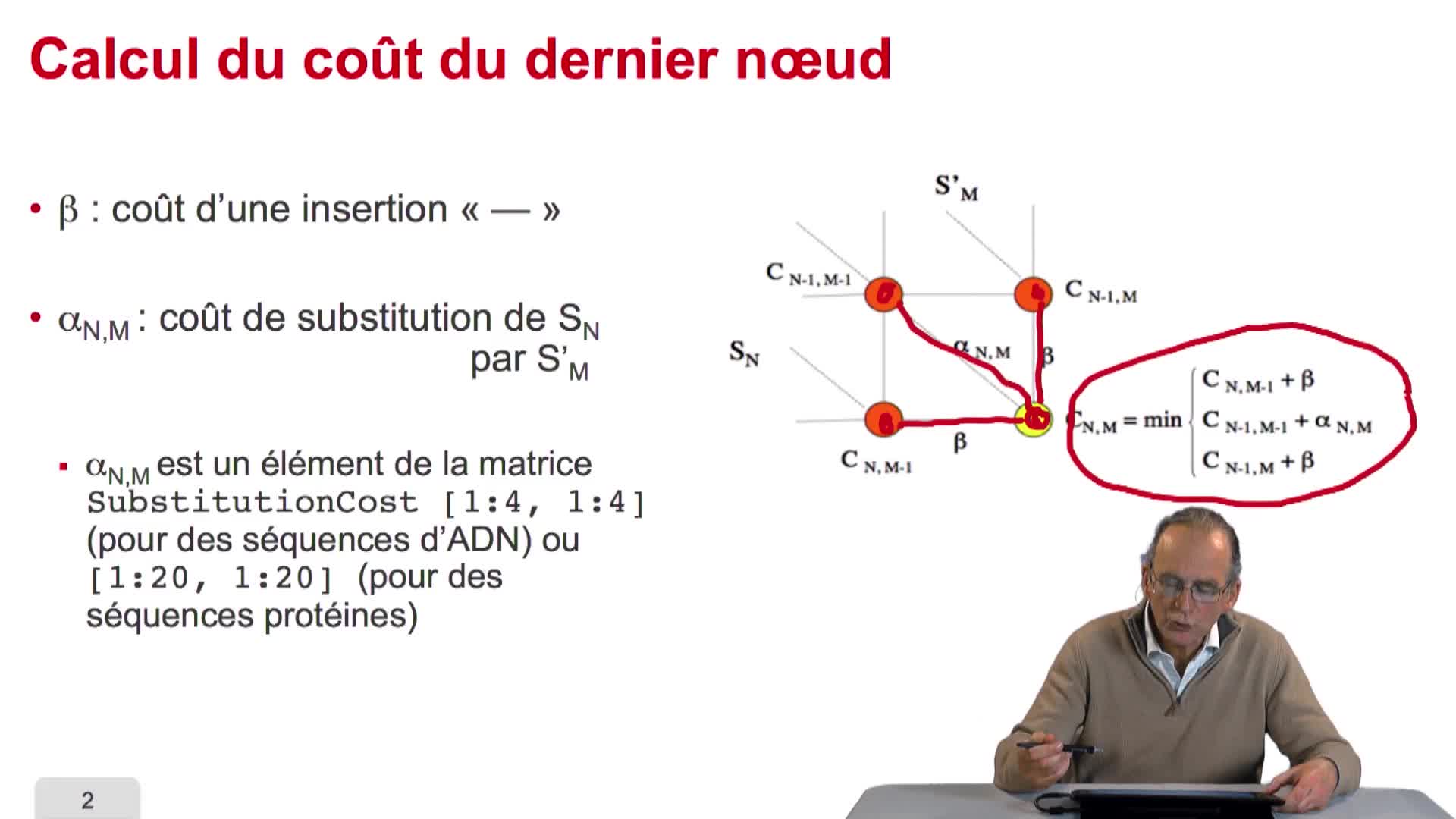
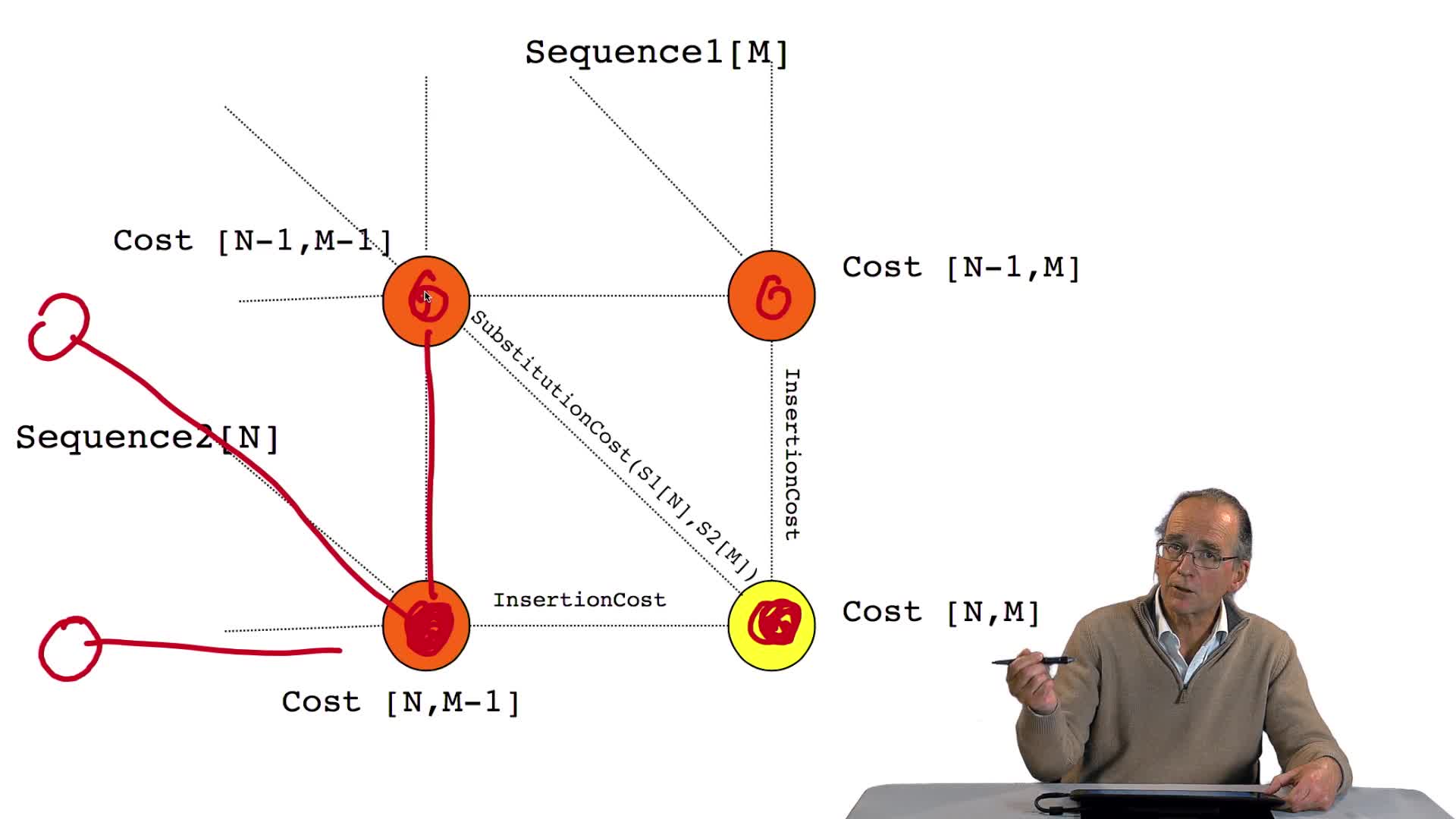
Nous avons vu l'ébauche de notre algorithme d'alignement optimal en considérant la possibilité de calculer le coût optimal, ou score optimal, de ce dernier noeud. Et nous avons vu que le coût de ce
-
4.1. Comment prédire les fonctions des gènes/protéines ?
RECHENMANN François
PARMENTELAT Thierry
Après avoir regardé dans les yeux, les semaines précédentes, l'ADN, vu comment cet ADN par séquençage produisait des textes, des séquences génomiques, étudié la relation entre gènes et protéines,
-
4.10. Cet algorithme est-il efficace ?
RECHENMANN François
PARMENTELAT Thierry
La version itérative de notre algorithme d'alignement optimal de séquences est indéniablement beaucoup plus efficace que sa version récursive, puisque nous avons vu qu'il permettait d'éviter que le
-
4.4. L’alignement de séquences devient un problème d’optimisation
RECHENMANN François
PARMENTELAT Thierry
La distance de Hamming nous donne une première possibilité de mesurer la similarité entre 2 séquences. Mais elle ne reflète pas suffisamment la réalité biologique. Qu'est-ce que j'entends par là ? On
-
4.8. Un algorithme récursif
RECHENMANN François
PARMENTELAT Thierry
Nous avons désormais en main tous les éléments pour écrire notre algorithme de détermination d'un alignement optimal, ici d'un chemin optimal. Avec les notations que nous avons introduites, je vous
-
4.2. Évolution et similarité de séquences
RECHENMANN François
PARMENTELAT Thierry
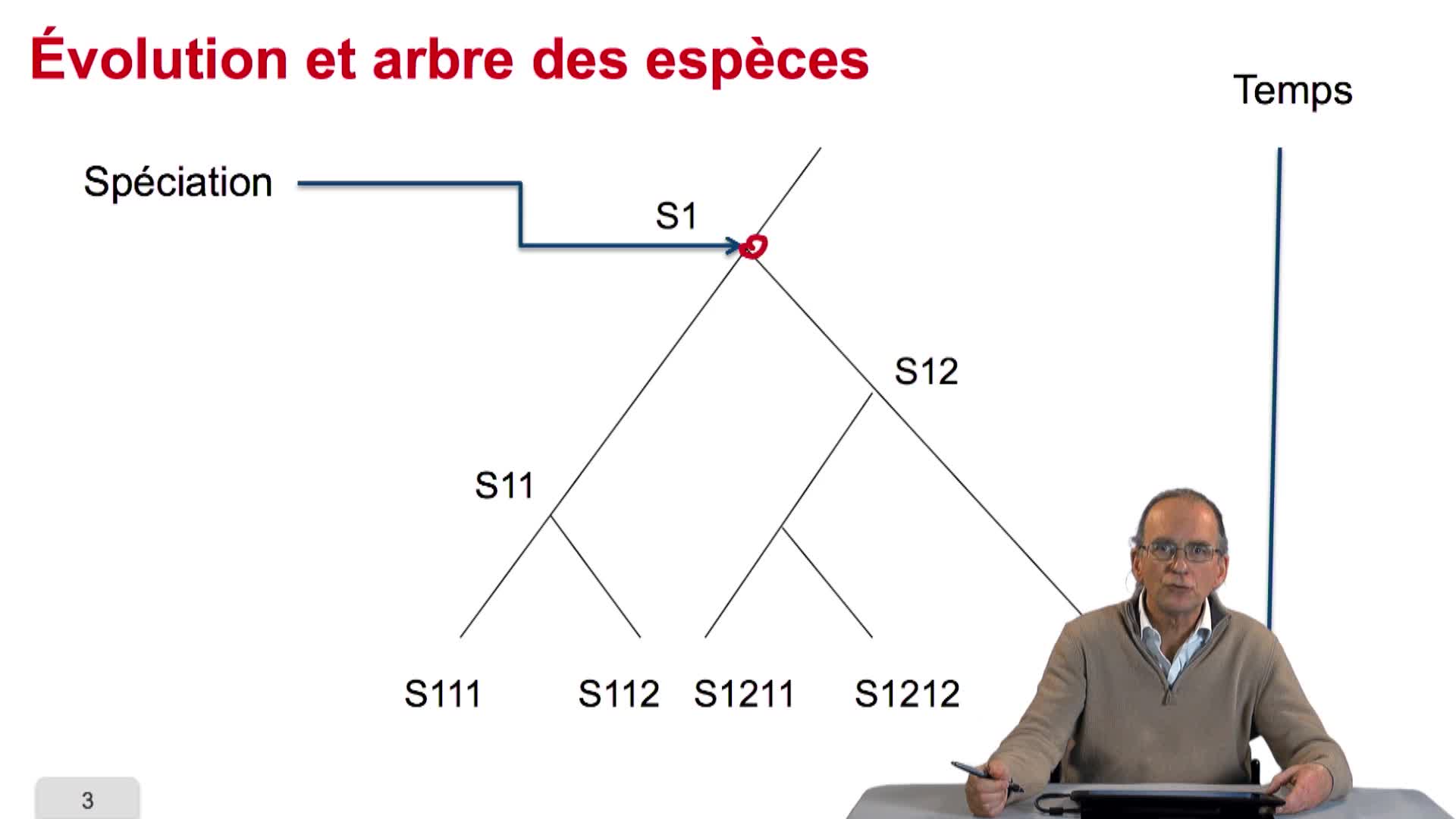
Avant de chercher à quantifier ce qu'est la similarité de séquence, on peut se poser la question même de savoir pourquoi des séquences de génome sont similaires entre organismes. La réponse tient dans
Avec les mêmes intervenants et intervenantes
-
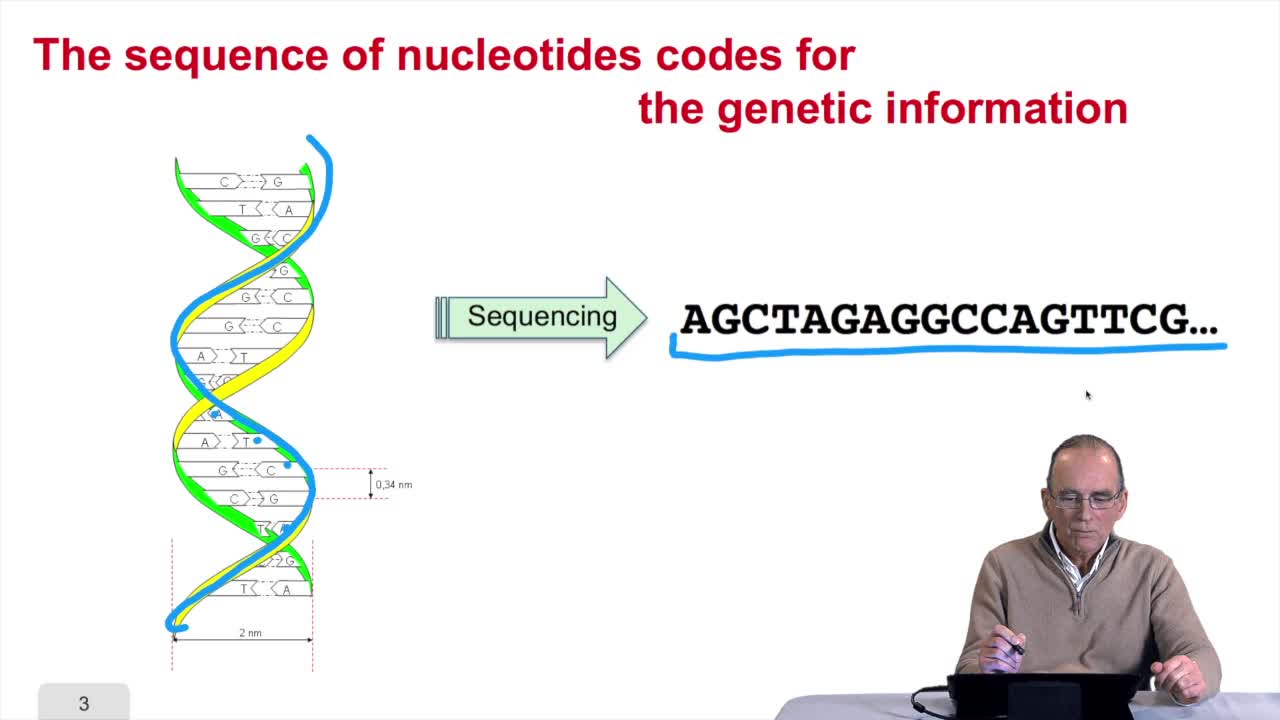
1.3. DNA codes for genetic information
RECHENMANN François
Remember at the heart of any cell,there is this very long molecule which is called a macromolecule for this reason, which is the DNA molecule. Now we will see that DNA molecules support what is called
-
2.1. The sequence as a model of DNA
RECHENMANN François
Welcome back to our course on genomes and algorithms that is a computer analysis ofgenetic information. Last week we introduced the very basic concept in biology that is cell, DNA, genome, genes
-
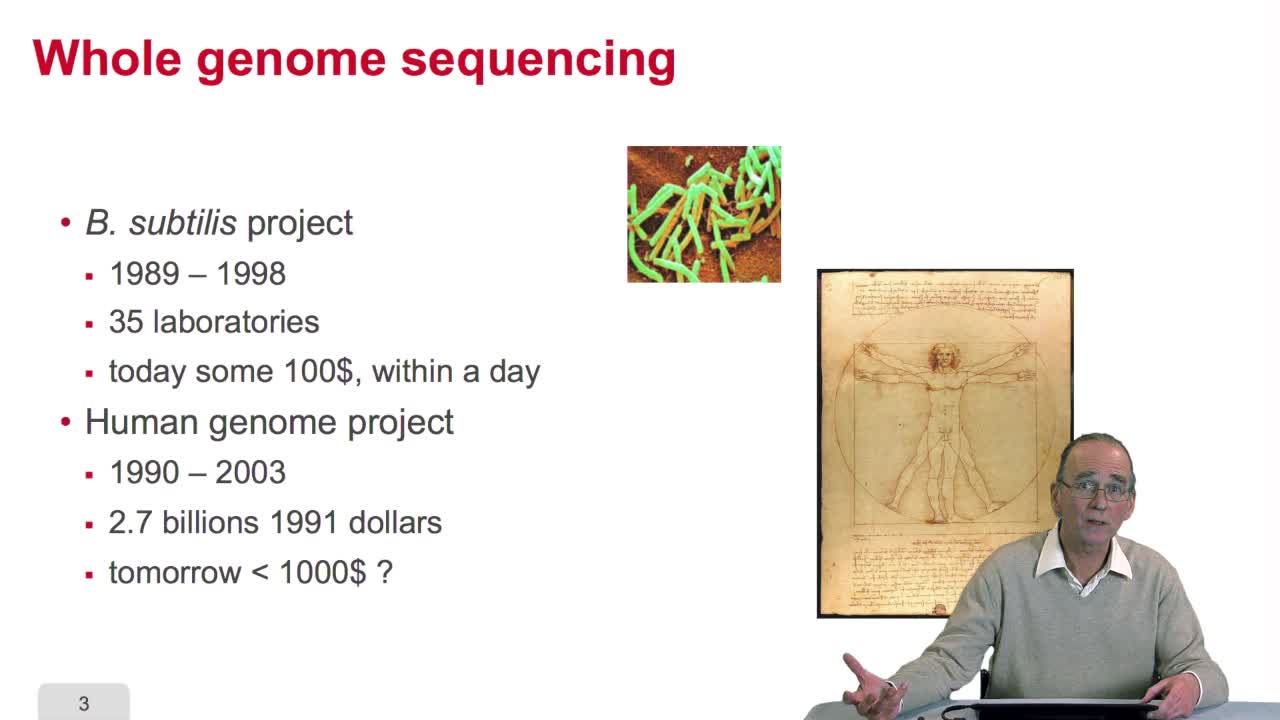
2.9. Whole genome sequencing
RECHENMANN François
Sequencing is anexponential technology. The progresses in this technologyallow now to a sequence whole genome, complete genome. What does it mean? Well let'stake two examples: some twenty years ago,
-
3.7. Index and suffix trees
RECHENMANN François
We have seen with the Boyer-Moore algorithm how we can increase the efficiency of spin searching through the pre-processing of the pattern to be searched. Now we will see that an alternative way of
-
4.4. Aligning sequences is an optimization problem
RECHENMANN François
We have seen a nice and a quitesimple solution for measuring the similarity between two sequences. It relied on the so-called hammingdistance that is counting the number of differencesbetween two
-
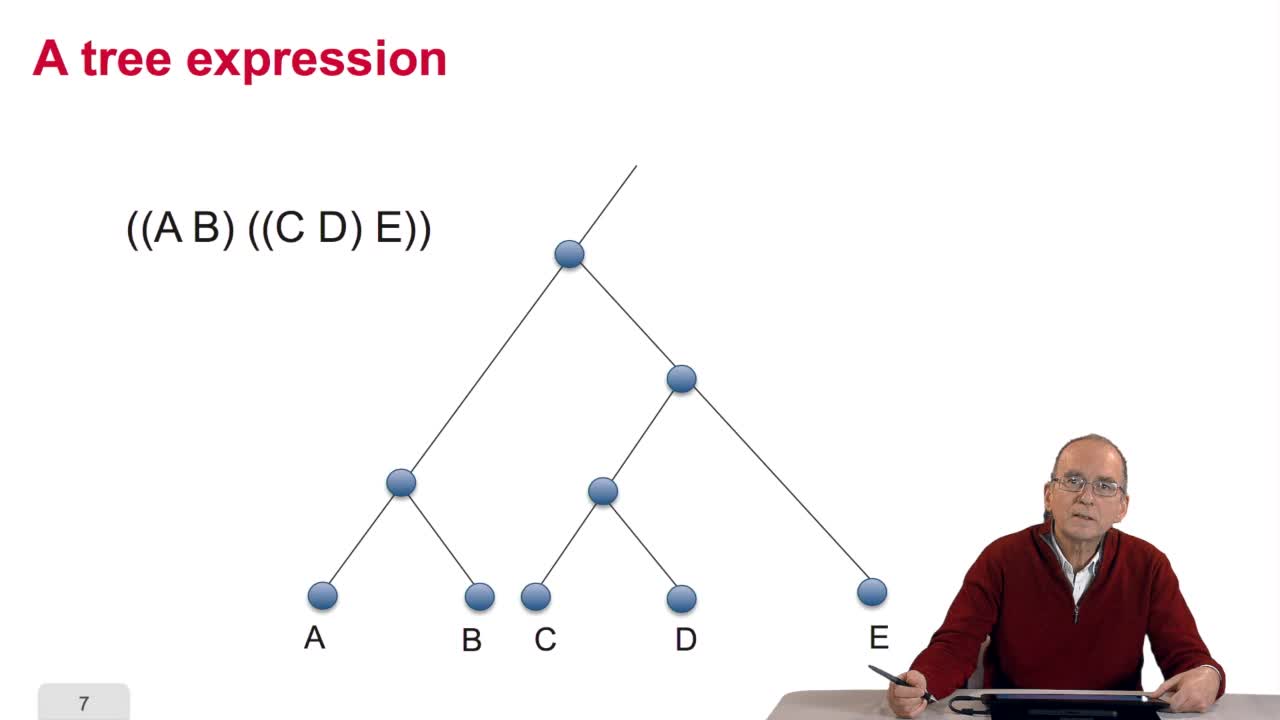
5.2. The tree, an abstract object
RECHENMANN François
When we speak of trees, of species,of phylogenetic trees, of course, it's a metaphoric view of a real tree. Our trees are abstract objects. Here is a tree and the different components of this tree.
-
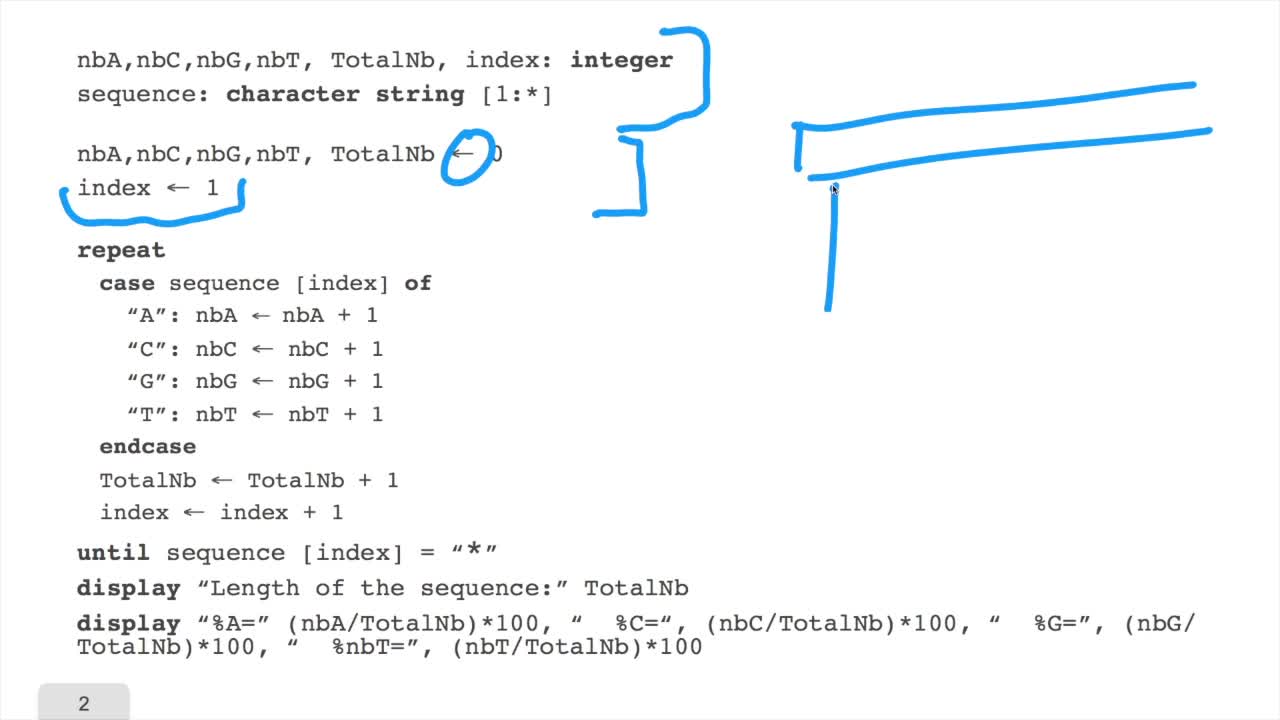
1.6. GC and AT contents of DNA sequence
RECHENMANN François
We have designed our first algorithmfor counting nucleotides. Remember, what we have writtenin pseudo code is first declaration of variables. We have several integer variables that are variables which
-
2.5. Implementing the genetic code
RECHENMANN François
Remember we were designing our translation algorithm and since we are a bit lazy, we decided to make the hypothesis that there was the adequate function forimplementing the genetic code. It's now time
-
3.2. A simple algorithm for gene prediction
RECHENMANN François
Based on the principle we statedin the last session, we will now write in pseudo code a firstalgorithm for locating genes on a bacterial genome. Remember first how this algorithm should work, we first
-
3.10. Gene prediction in eukaryotic genomes
RECHENMANN François
If it is possible to have verygood predictions for bacterial genes, it's certainly not the caseyet for eukaryotic genomes. Eukaryotic cells have manydifferences in comparison to prokaryotic cells. You
-
4.8. A recursive algorithm
RECHENMANN François
We have seen how we can computethe optimal cost, the ending node of our grid if we know the optimal cost of the three adjacent nodes. This is this computation scheme we can see here using the notation
-
5.6. The diversity of bioinformatics algorithms
RECHENMANN François
In this course, we have seen a very little set of bioinformatic algorithms. There exist numerous various algorithms in bioinformatics which deal with a large span of classes of problems. For example,
Sur le même thème
-
The tree of life
ABBY Sophie
Les Rencontres Exobiologiques pour Doctorants (RED) sont une école de formation sur les « bases de l'astrobiologie ». L’édition 2025 s’est tenue du 16 au 21 mars au Parc Ornithologique du Teich.
-
Machines algorithmiques, mythes et réalités
MAZENOD Vincent
Vincent Mazenod, informaticien, partage le fruit de ses réflexions sur l'évolution des outils numériques, en lien avec les problématiques de souveraineté, de sécurité et de vie privée...
-
Désassemblons le numérique - #Episode11 : Les algorithmes façonnent-ils notre société ?
SCHWARTZ Arnaud
LIMA PILLA Laércio
ESTéRIE Pierre
SALLET Frédéric
FERBOS Aude
ROUMANOS Rayya
CHRAIBI KADOUD Ikram
Un an après le tout premier hackathon sur les méthodologies d'enquêtes journalistiques sur les algorithmes, ce nouvel épisode part à la rencontre de différents points de vue sur les algorithmes.
-
Les machines à enseigner. Du livre à l'IA...
BRUILLARD Éric
Que peut-on, que doit-on déléguer à des machines ? C'est l'une des questions explorées par Éric Bruillard qui, du livre aux IA génératives, expose l'évolution des machines à enseigner...
-
Désassemblons le numérique - #Episode9 : Bientôt des supercalculateurs dans nos piscines ?
BEAUMONT Olivier
BOUZEL Rémi
Des supercalculateurs feraient-ils bientôt leur apparition dans les piscines municipales pour les chauffer ? Réponses d'Olivier Beaumont, responsable de l'équipe-projet Topal, et Rémi Bouzel,
-
Le projet dnarXiv : Stockage de données sur des molécules d'ADN
LAVENIER Dominique
DUPRAZ Elsa
LEBLANC Julien
COATRIEUX Gouenou
Dominique Lavenier, Elsa Dupraz, Julien Leblanc et Gouenou Coatrieux nous présentent le projet dnarXiv, un projet porté par le LabEx CominLabs qui explore le stockage de données sur des molécules d
-
Projection methods for community detection in complex networks
LITVAK Nelly
Community detection is one of most prominent tasks in the analysis of complex networks such as social networks, biological networks, and the world wide web. A community is loosely defined as a group
-
Lara Croft. doing fieldwork under surveillance
DALL'AGNOLA Jasmin
Lara Croft. Doing Fieldwork Under Surveillance Intervention de Jasmin Dall'Agnola (The George Washington University), dans le cadre du Colloque coorganisé par Anders Albrechtslund, professeur en
-
Containing predictive tokens in the EU
CZARNOCKI Jan
Containing Predictive Tokens in the EU – Mapping the Laws Against Digital Surveillance, intervention de Jan Czarnocki (KU Leuven), dans le cadre du Colloque coorganisé par Anders Albrechtslund,
-
Ivan Murit - Processus de création d'images
MURIT Ivan
Je vais présenter une manière décalée d'aborder les outils d'impression. Pour cela nous ne partirons pas de l'envie d'imprimer une image préexistante, mais d'avant cela : comment se crée une forme
-
Le Creativ’Lab, au cœur de la robotique et de l’intelligence artificielle (ASR N°18 - LORIA)
HéNAFF Patrick
LEFEBVRE Sylvain
Le LORIA, laboratoire phare de la Grande Région dans le domaine de l’informatique, propose de rendre la recherche plus ouverte, plus collaborative, plus ambitieuse… en un mot, plus créative, à travers
-
Les algorithmes de Parcoursup
MATHIEU Claire
L’objectif de la journée « Algorithmes d’aide à la décision publique » était de sensibiliser le grand public aux rôles des algorithmes d’aide à la décision publique utilisés par exemple pour l