Notice
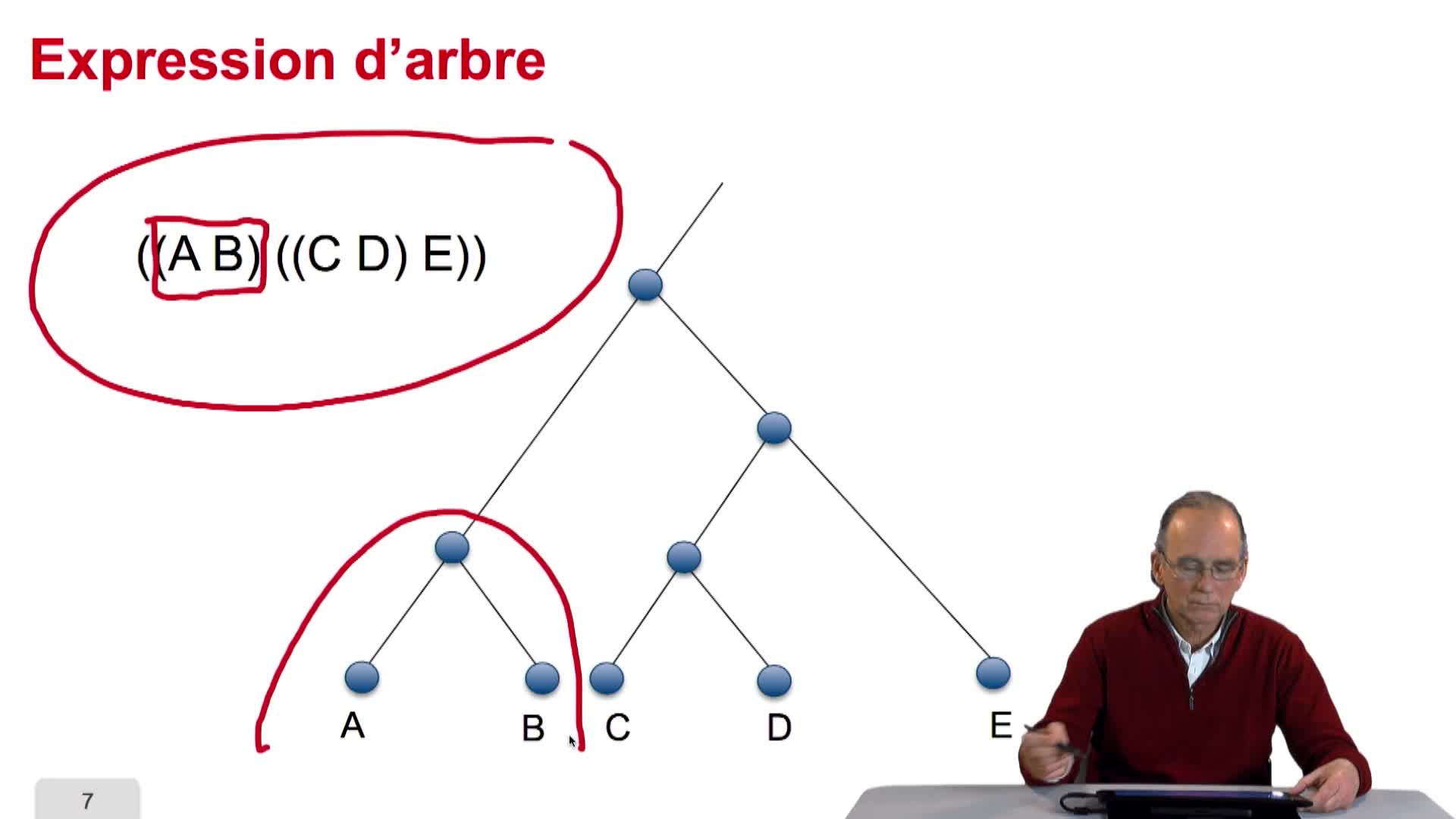
5.4. L’algorithme UPGMA
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
L'algorithme, que nous allons étudier pour la reconstruction d'arbres phylogénétiques à partir des distances, s'appelle UPGMA. Un nom plutôt compliqué pour une méthode qui est plutôt simple. Et même, on le verra trop simple. UPGMA signifie Unweighted Pair Group Method with Arithmetic Mean. Nous allons voir au fur et à mesure, la signification dans l'exécution de l'algorithme de chacun de ces termes. Le point de départ de cet algorithme est donc un tableau de distances, tel que nous avons pu le remplir dans la session précédente. Voilà l'exemple que nous allons traiter. C'est un exemple simple. Nous avons sept espèces différentes et nous avons calculé les distances entre ces espèces à travers le calcul des distances, entre les séquences d'un gène homologue de ces espèces, à toutes ces espèces. Vous vous souvenez que le tableau que nous avons calculé était d'une part symétrique et que d'autre part, les valeurs sur la diagonale étaient sans surprise égales à 0. Ici nous avons choisi de ne conserver et de n'afficher que les valeurs significatives. Donc inutile de montrer les valeurs qui sont les symétriques des autres. Et inutile d'afficher les 0 sur les diagonales. Ce qui explique que notre tableau apparaît incomplet d'une certaine manière. La première étape de l'algorithme consiste à rechercher parmi toutes ces valeurs de distance dans le tableau la plus petite. Ici, c'est 2 et c'est la distance qui sépare l'espèce F de l'espèce C. Raccourci de langage, la distance qui sépare les séquences associées aux espèces F et C. C'est la distance la plus faible. Elle nous pousse donc à grouper ces 2 espèces dans un même sous-graphe en créant un noeud ancêtre ici. Ces 2 espèces sont proches, sont similaires parce qu'elles possèdent un ancêtre commun récent...
ERRATUM
Sur la slide 3 l’orateur parle de 7 espèces différentes, en fait il y en a 6.
Intervention / Responsable scientifique
Dans la même collection
-
5.7. Les applications en microbiologie
RechenmannFrançoisParmentelatThierryUne très grande diversité, on l'a vu, d'algorithmes en bio-informatique, motivé par la résolution de problèmes différents. Ces algorithmes, ces recherches en bio-informatique, s'appuient sur des
-
5.1. L’arbre des espèces
RechenmannFrançoisParmentelatThierryDans cette cinquième et dernière partie de notre cours sur le génome et les algorithmes, qui se veut une introduction à l'analyse informatique de l'information génétique, nous regarderons de plus près
-
5.5. Quand les différences sont trompeuses
RechenmannFrançoisParmentelatThierryIl y a plusieurs raisons pour lesquelles la méthode UPGMA, que nous venons de voir, se révèle simpliste. L'une des raisons par exemple, c'est pourquoi quand on recalcule les distances, quand on a
-
5.2. L’arbre, objet abstrait
RechenmannFrançoisParmentelatThierryVous l'aurez compris un arbre phylogénétique est un arbre abstrait qui n'a qu'un lointain rapport métaphorique avec un véritable arbre. L'arbre des bio-informaticiens et des informaticiens se
-
5.6. La diversité des algorithmes informatiques
RechenmannFrançoisParmentelatThierryNous n'avons vu dans ce cours qu'un exemple extrêmement réduit d'algorithme bio informatique. Il existe en effet une très grande diversité de ces algorithmes bio informatiques qui sont motivés par l
-
5.3. Remplir un tableau de distances
RechenmannFrançoisParmentelatThierryPour tenter de construire l'arbre phylogénétique d'un ensemble d'espèces, nous allons utiliser les données et génotypique ou des données génotypiques disponibles sur ces espèces. Plus clairement, nous
Avec les mêmes intervenants et intervenantes
-
1.4. What is an algorithm?
RechenmannFrançoisWe have seen that a genomic textcan be indeed a very long sequence of characters. And to interpret this sequence of characters, we will need to use computers. Using computers means writing program.
-
2.2. Genes: from Mendel to molecular biology
RechenmannFrançoisThe notion of gene emerged withthe works of Gregor Mendel. Mendel studied the inheritance on some traits like the shape of pea plant seeds,through generations. He stated the famous laws of inheritance
-
2.10. How to find genes?
RechenmannFrançoisGetting the sequence of the genome is only the beginning, as I explained, once you have the sequence what you want to do is to locate the gene, to predict the function of the gene and maybe study the
-
3.8. Probabilistic methods
RechenmannFrançoisUp to now, to predict our gene,we only rely on the process of searching certain strings or patterns. In order to further improve our gene predictor, the idea is to use, to rely onprobabilistic methods
-
4.3. Measuring sequence similarity
RechenmannFrançoisSo we understand why gene orprotein sequences may be similar. It's because they evolve togetherwith the species and they evolve in time, there aremodifications in the sequence and that the sequence
-
5.3. Building an array of distances
RechenmannFrançoisSo using the sequences of homologous gene between several species, our aim is to reconstruct phylogenetic tree of the corresponding species. For this, we have to comparesequences and compute distances
-
1.7. DNA walk
RechenmannFrançoisWe will now design a more graphical algorithm which is called "the DNA walk". We shall see what does it mean "DNA walk". Walk on to DNA. Something like that, yes. But first, just have a look again at
-
2.6. Algorithms + data structures = programs
RechenmannFrançoisBy writing the Lookup GeneticCode Function, we completed our translation algorithm. So we may ask the question about the algorithm, does it terminate? Andthe answer is yes, obviously. Is it pertinent,
-
3.3. Searching for start and stop codons
RechenmannFrançoisWe have written an algorithm for finding genes. But you remember that we arestill to write the two functions for finding the next stop codonand the next start codon. Let's see how we can do that. We
-
4.1. How to predict gene/protein functions?
RechenmannFrançoisLast week we have seen that annotating a genome means first locating the genes on the DNA sequences that is the genes, the region coding for proteins. But this is indeed the first step,the next very
-
4.10. How efficient is this algorithm?
RechenmannFrançoisWe have seen the principle of an iterative algorithm in two paths for aligning and comparing two sequences of characters, here DNA sequences. And we understoodwhy the iterative version is much more
-
5.7. The application domains in microbiology
RechenmannFrançoisBioinformatics relies on many domains of mathematics and computer science. Of course, algorithms themselves on character strings are important in bioinformatics, we have seen them. Algorithms and
Sur le même thème
-
La voix, une donnée identifiante à protéger
VincentEmmanuelEmmanuel Vincent, chercheur au Centre Inria de l'Université de Lorraine et au Loria (Laboratoire lorrain de recherche en informatique et ses applications), présente sa recherche sur l'anonymisation de
-
Podcast 1/4 d'heure avec : Emmanuel Vincent, chercheur au Centre Inria de l'Université de Lorraine …
VincentEmmanuelRencontre avec Emmanuel Vincent - chercheur au Centre Inria de l'Université de Lorraine et Loria (Laboratoire lorrain de recherche en informatique et ses applications).
-
Stockage de données numériques sur ADN synthétique : Introduction au domaine
AntoniniMarcDuprazElsaLavenierDominiquePrésentation globale des différentes étapes du stockage de données sur des molécules d'ADN synthétique
-
Stockage de données numériques sur ADN synthétique : Production des données: synthèse, séquençage
LavenierDominiqueBarbryPascalDescription des opérations d'écriture et de lecture des molécules d'ADN : synthèse et séquençage.
-
Stockage de données numériques sur ADN synthétique : Reconstruction des données
LavenierDominiqueTraitement des données après séquençage
-
Stockage de données numériques sur ADN synthétique : Codage Canal
DuprazElsaTechniques de codage pour le stockage de données sur ADN
-
Stockage de données numériques sur ADN synthétique : Codage Source
AntoniniMarcCodage source pour le stockage de données sur ADN synthétique
-
Stockage de données numériques sur ADN synthétique : Théorie de l'information
Kas HannaSergeQuelle quantité d'information peut-on stocker et récupérer de manière fiable dans l'ADN ?
-
The tree of life
AbbySophieLes Rencontres Exobiologiques pour Doctorants (RED) sont une école de formation sur les « bases de l'astrobiologie ». L’édition 2025 s’est tenue du 16 au 21 mars au Parc Ornithologique du Teich.
-
Machines algorithmiques, mythes et réalités
MazenodVincentVincent Mazenod, informaticien, partage le fruit de ses réflexions sur l'évolution des outils numériques, en lien avec les problématiques de souveraineté, de sécurité et de vie privée...
-
Désassemblons le numérique - #Episode11 : Les algorithmes façonnent-ils notre société ?
SchwartzArnaudLima PillaLaércioEstériePierreSalletFrédéricFerbosAudeRoumanosRayyaChraibi KadoudIkramUn an après le tout premier hackathon sur les méthodologies d'enquêtes journalistiques sur les algorithmes, ce nouvel épisode part à la rencontre de différents points de vue sur les algorithmes.
-
Les machines à enseigner. Du livre à l'IA...
BruillardÉricQue peut-on, que doit-on déléguer à des machines ? C'est l'une des questions explorées par Éric Bruillard qui, du livre aux IA génératives, expose l'évolution des machines à enseigner...