Notice
4.3. Quantifier la similarité de deux séquences
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
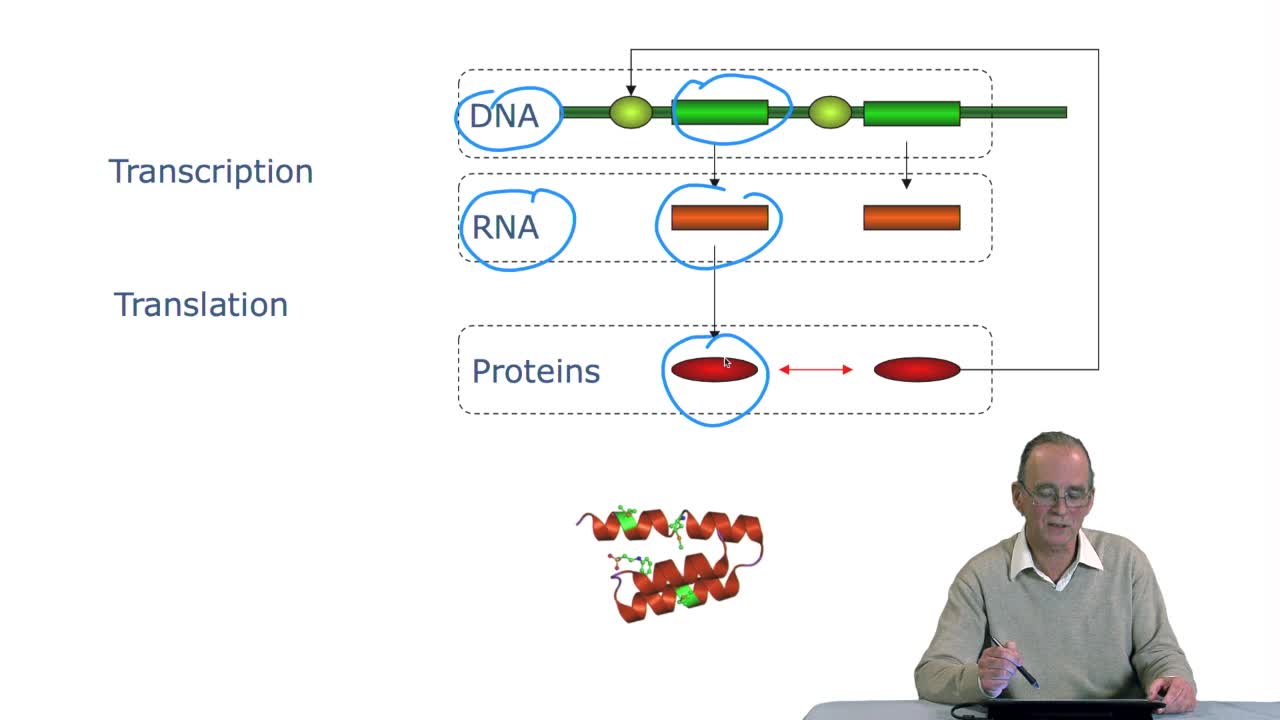
Le principe est donc de rechercher, dans les bases de données, des séquences similaires à celles que nous sommes en train d'étudier. Nous faisons aussi l'hypothèse que plus les séquences sont similaires, meilleure est la pertinence de l'information attachée à la séquence retrouvée dans la base de données.
Nous allons donc chercher un moyen de quantifier le niveau de similarité entre 2 séquences. Le premier moyen très simple, c'est d'utiliser la distance dite de Hamming. De quoi s'agit-il ? Très simple, en effet. Prenez ces 2 séquences ici. Vous pouvez très rapidement à l'oeil voir qu'elles diffèrent par 2 substitutions, 2 différences, ça va être la distance de Hamming. De même, cette paire ici, 3 substitutions, distance de Hamming, 3.
Est-ce une distance véritablement au sens mathématique du terme ? Je vous rappelle les 3 propriétés qu'une distance mathématique doit satisfaire : la distance d'une séquence à elle-même doit être nulle, ce qui est le cas, puisqu'il n'y a pas de différence entre les 2, pas de substitution ni quoi que ce soit, distance 0. La distance entre une séquence et une seconde séquence doit être la même qu'entre la seconde et la première. Bien entendu, le nombre de différences reste le même. Et la 3ème qui est dite l'inégalité qui doit être effectivement vérifiée elle aussi, ce que l'on peut faire assez facilement en prenant quelques exemples. C'est donc bien une distance au sens mathématique...
Intervention / Responsable scientifique
Dans la même collection
-
4.7. Coûts et alignement
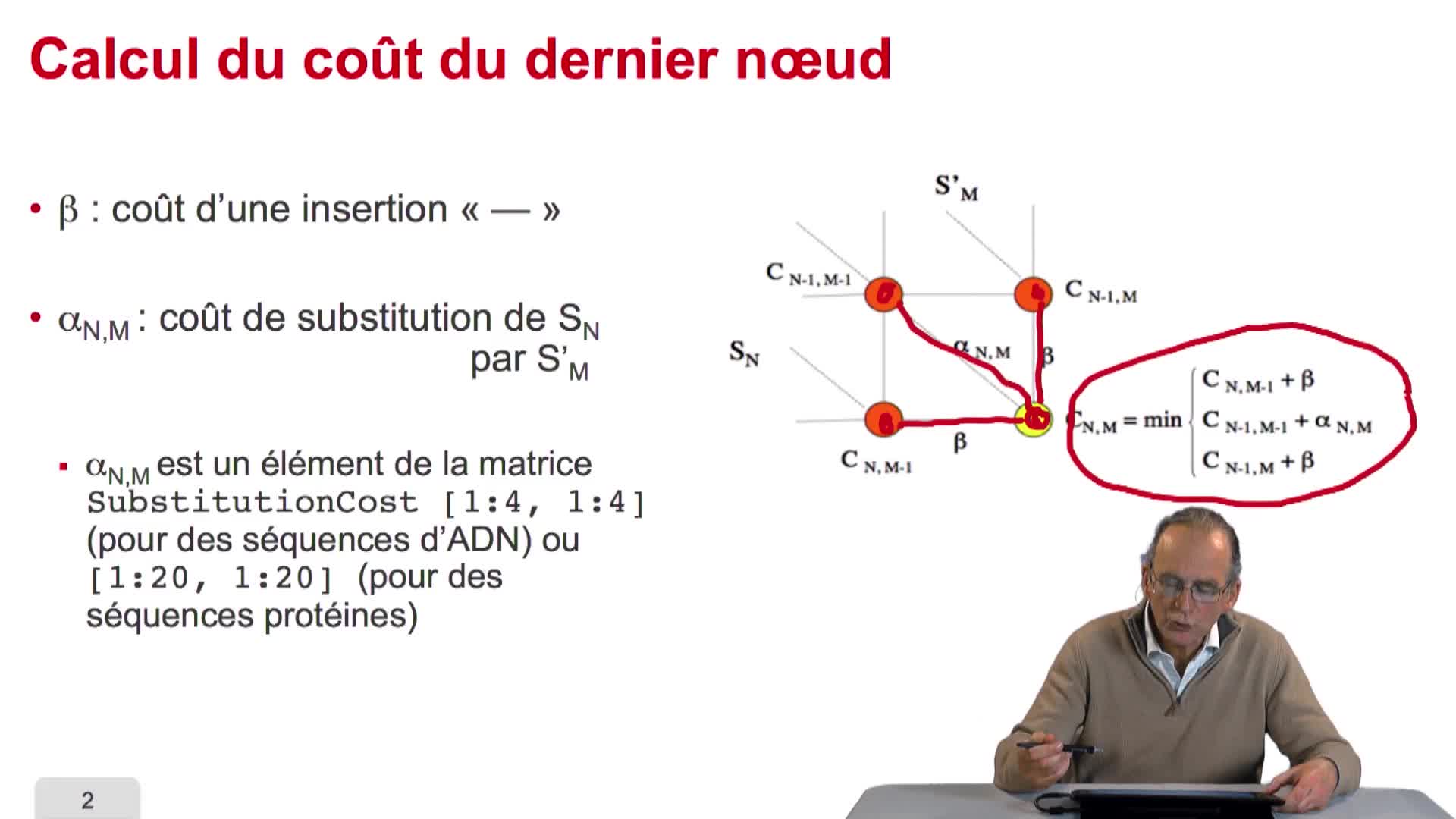
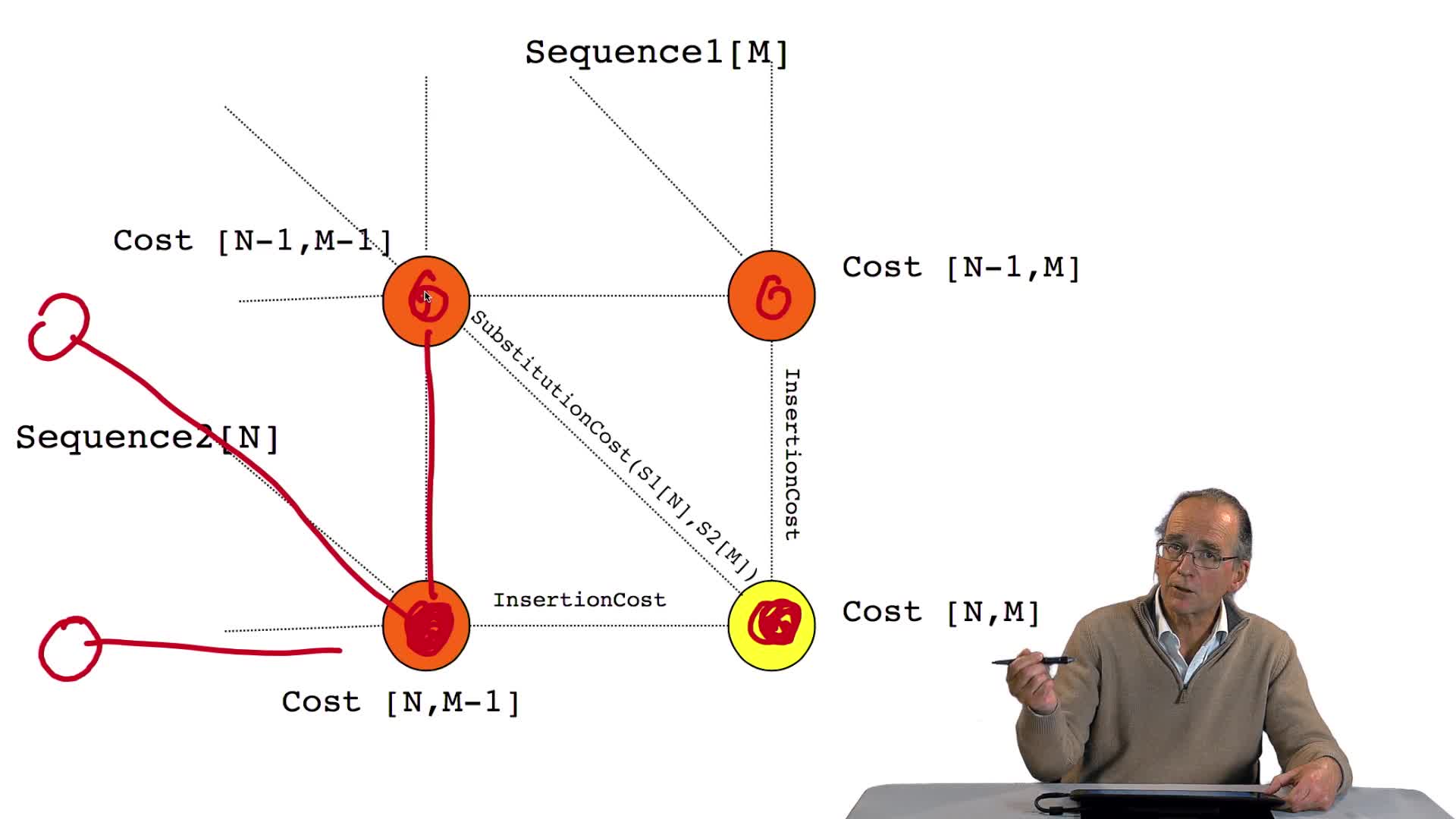
RechenmannFrançoisParmentelatThierryNous avons vu l'ébauche de notre algorithme d'alignement optimal en considérant la possibilité de calculer le coût optimal, ou score optimal, de ce dernier noeud. Et nous avons vu que le coût de ce
-
4.1. Comment prédire les fonctions des gènes/protéines ?
RechenmannFrançoisParmentelatThierryAprès avoir regardé dans les yeux, les semaines précédentes, l'ADN, vu comment cet ADN par séquençage produisait des textes, des séquences génomiques, étudié la relation entre gènes et protéines,
-
4.10. Cet algorithme est-il efficace ?
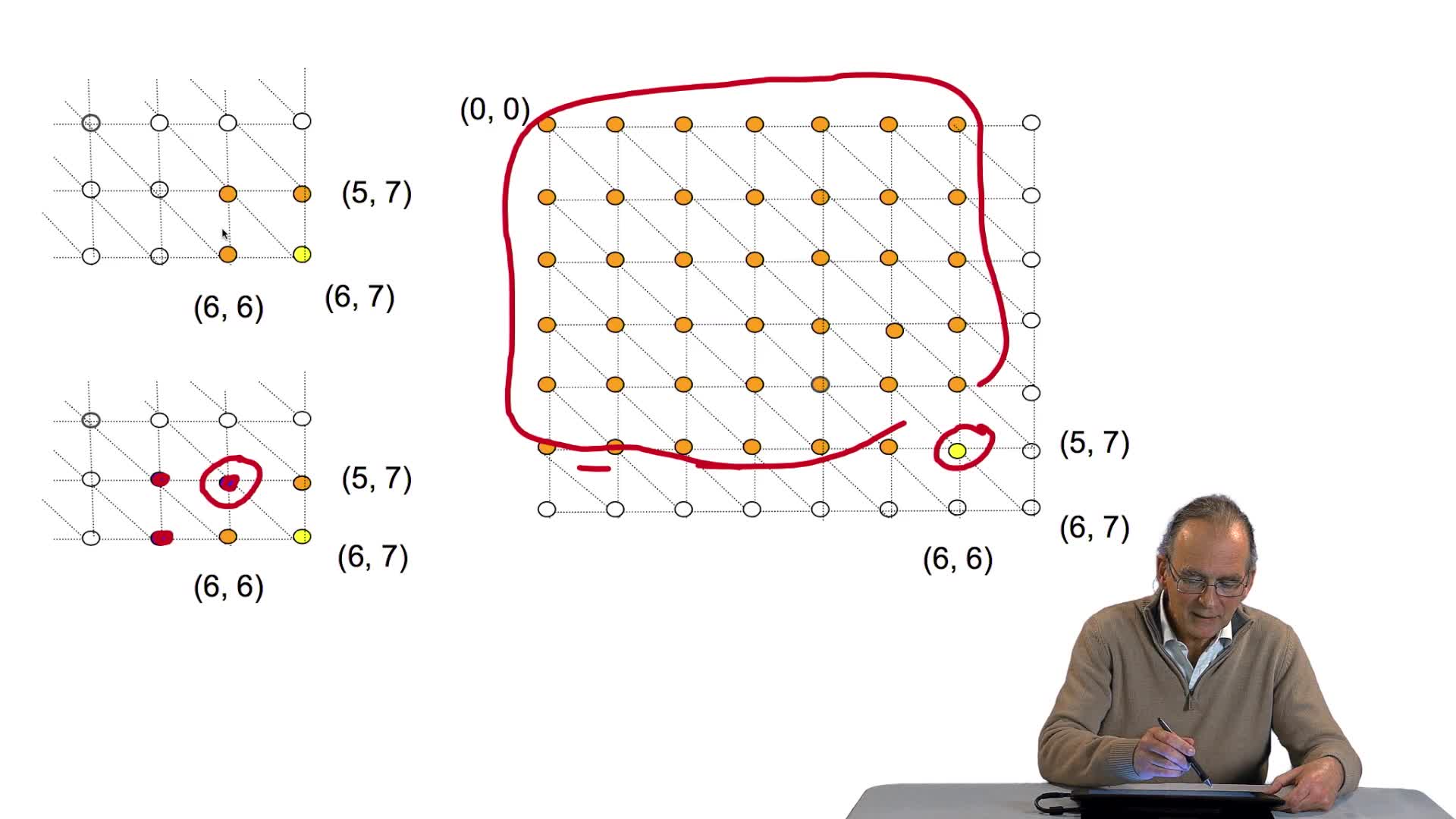
RechenmannFrançoisParmentelatThierryLa version itérative de notre algorithme d'alignement optimal de séquences est indéniablement beaucoup plus efficace que sa version récursive, puisque nous avons vu qu'il permettait d'éviter que le
-
4.5. Un alignement de séquences vu comme un chemin dans une grille
RechenmannFrançoisParmentelatThierryPour comparer deux séquences entre elles, il faut donc les aligner. Aligner ces deux séquences suppose faire des hypothèses d'insertion, délétion, aux bons endroits. Ça signifie, d'un point de vue
-
4.8. Un algorithme récursif
RechenmannFrançoisParmentelatThierryNous avons désormais en main tous les éléments pour écrire notre algorithme de détermination d'un alignement optimal, ici d'un chemin optimal. Avec les notations que nous avons introduites, je vous
-
4.2. Évolution et similarité de séquences
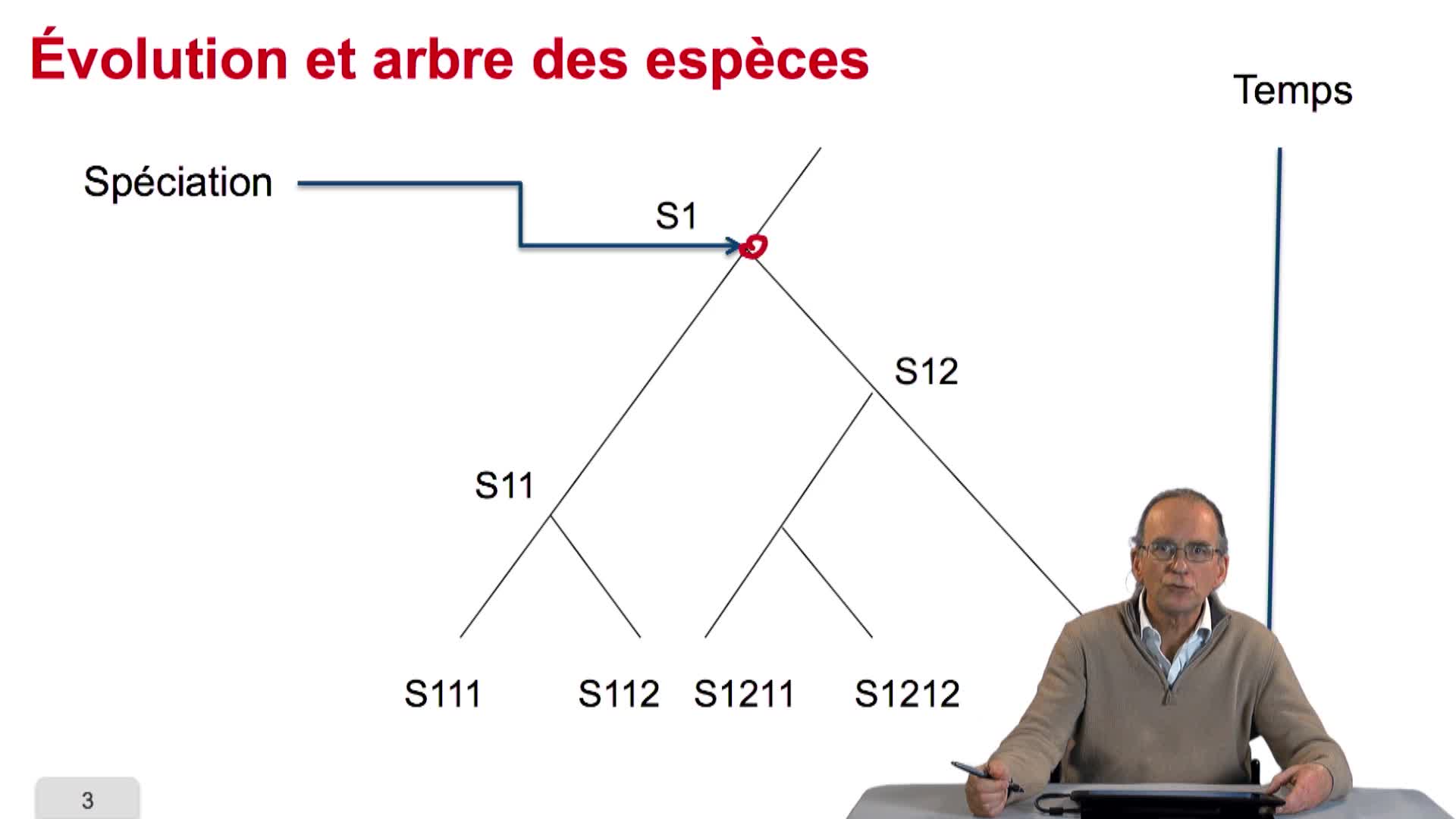
RechenmannFrançoisParmentelatThierryAvant de chercher à quantifier ce qu'est la similarité de séquence, on peut se poser la question même de savoir pourquoi des séquences de génome sont similaires entre organismes. La réponse tient dans
-
4.6. Si un chemin est optimal, tous ses chemins partiels sont optimaux
RechenmannFrançoisParmentelatThierryNous cherchons à concevoir un algorithme capable de déterminer l'alignement optimal de 2 séquences. Et nous avons vu que ça revient à chercher un algorithme qui recherche un chemin optimal dans une
-
4.9. Éviter la récursivité : une version itérative
RechenmannFrançoisParmentelatThierryLa fonction récursive que nous avons obtenue est d'un code assez compact et plutôt élégant, mais effectivement peu efficace. Pourquoi ? Rappelons son fonctionnement. Cette fonction est d'abord appelée
-
4.4. L’alignement de séquences devient un problème d’optimisation
RechenmannFrançoisParmentelatThierryLa distance de Hamming nous donne une première possibilité de mesurer la similarité entre 2 séquences. Mais elle ne reflète pas suffisamment la réalité biologique. Qu'est-ce que j'entends par là ? On
Avec les mêmes intervenants et intervenantes
-
1.7. DNA walk
RechenmannFrançoisWe will now design a more graphical algorithm which is called "the DNA walk". We shall see what does it mean "DNA walk". Walk on to DNA. Something like that, yes. But first, just have a look again at
-
2.6. Algorithms + data structures = programs
RechenmannFrançoisBy writing the Lookup GeneticCode Function, we completed our translation algorithm. So we may ask the question about the algorithm, does it terminate? Andthe answer is yes, obviously. Is it pertinent,
-
3.3. Searching for start and stop codons
RechenmannFrançoisWe have written an algorithm for finding genes. But you remember that we arestill to write the two functions for finding the next stop codonand the next start codon. Let's see how we can do that. We
-
4.1. How to predict gene/protein functions?
RechenmannFrançoisLast week we have seen that annotating a genome means first locating the genes on the DNA sequences that is the genes, the region coding for proteins. But this is indeed the first step,the next very
-
4.10. How efficient is this algorithm?
RechenmannFrançoisWe have seen the principle of an iterative algorithm in two paths for aligning and comparing two sequences of characters, here DNA sequences. And we understoodwhy the iterative version is much more
-
5.7. The application domains in microbiology
RechenmannFrançoisBioinformatics relies on many domains of mathematics and computer science. Of course, algorithms themselves on character strings are important in bioinformatics, we have seen them. Algorithms and
-
1.2. At the heart of the cell: the DNA macromolecule
RechenmannFrançoisDuring the last session, we saw how at the heart of the cell there's DNA in the nucleus, sometimes of cells, or directly in the cytoplasm of the bacteria. The DNA is what we call a macromolecule, that
-
1.10. Overlapping sliding window
RechenmannFrançoisWe have made some drawings along a genomic sequence. And we have seen that although the algorithm is quite simple, even if some points of the algorithmare bit trickier than the others, we were able to
-
2.3. The genetic code
RechenmannFrançoisGenes code for proteins. What is the correspondence betweenthe genes, DNA sequences, and the structure of proteins? The correspondence isthe genetic code. Proteins have indeedsequences of amino acids.
-
3.6. Boyer-Moore algorithm
RechenmannFrançoisWe have seen how we can make gene predictions more reliable through searching for all the patterns,all the occurrences of patterns. We have seen, for example, howif we locate the RBS, Ribosome
-
4.5. A sequence alignment as a path
RechenmannFrançoisComparing two sequences and thenmeasuring their similarities is an optimization problem. Why? Because we have seen thatwe have to take into account substitution and deletion. During the alignment, the
-
5.5. Differences are not always what they look like
RechenmannFrançoisThe algorithm we have presented works on an array of distance between sequences. These distances are evaluated on the basis of differences between the sequences. The problem is that behind the
Sur le même thème
-
The tree of life
AbbySophieLes Rencontres Exobiologiques pour Doctorants (RED) sont une école de formation sur les « bases de l'astrobiologie ». L’édition 2025 s’est tenue du 16 au 21 mars au Parc Ornithologique du Teich.
-
Machines algorithmiques, mythes et réalités
MazenodVincentVincent Mazenod, informaticien, partage le fruit de ses réflexions sur l'évolution des outils numériques, en lien avec les problématiques de souveraineté, de sécurité et de vie privée...
-
Désassemblons le numérique - #Episode11 : Les algorithmes façonnent-ils notre société ?
SchwartzArnaudLima PillaLaércioEstériePierreSalletFrédéricFerbosAudeRoumanosRayyaChraibi KadoudIkramUn an après le tout premier hackathon sur les méthodologies d'enquêtes journalistiques sur les algorithmes, ce nouvel épisode part à la rencontre de différents points de vue sur les algorithmes.
-
Les machines à enseigner. Du livre à l'IA...
BruillardÉricQue peut-on, que doit-on déléguer à des machines ? C'est l'une des questions explorées par Éric Bruillard qui, du livre aux IA génératives, expose l'évolution des machines à enseigner...
-
Désassemblons le numérique - #Episode9 : Bientôt des supercalculateurs dans nos piscines ?
BeaumontOlivierBouzelRémiDes supercalculateurs feraient-ils bientôt leur apparition dans les piscines municipales pour les chauffer ? Réponses d'Olivier Beaumont, responsable de l'équipe-projet Topal, et Rémi Bouzel,
-
Le projet dnarXiv : Stockage de données sur des molécules d'ADN
LavenierDominiqueDuprazElsaLeblancJulienCoatrieuxGouenouDominique Lavenier, Elsa Dupraz, Julien Leblanc et Gouenou Coatrieux nous présentent le projet dnarXiv, un projet porté par le LabEx CominLabs qui explore le stockage de données sur des molécules d
-
Projection methods for community detection in complex networks
LitvakNellyCommunity detection is one of most prominent tasks in the analysis of complex networks such as social networks, biological networks, and the world wide web. A community is loosely defined as a group
-
Lara Croft. doing fieldwork under surveillance
Dall'AgnolaJasminLara Croft. Doing Fieldwork Under Surveillance Intervention de Jasmin Dall'Agnola (The George Washington University), dans le cadre du Colloque coorganisé par Anders Albrechtslund, professeur en
-
Containing predictive tokens in the EU
CzarnockiJanContaining Predictive Tokens in the EU – Mapping the Laws Against Digital Surveillance, intervention de Jan Czarnocki (KU Leuven), dans le cadre du Colloque coorganisé par Anders Albrechtslund,
-
Ivan Murit - Processus de création d'images
MuritIvanJe vais présenter une manière décalée d'aborder les outils d'impression. Pour cela nous ne partirons pas de l'envie d'imprimer une image préexistante, mais d'avant cela : comment se crée une forme
-
Le Creativ’Lab, au cœur de la robotique et de l’intelligence artificielle (ASR N°18 - LORIA)
HénaffPatrickLefebvreSylvainLe LORIA, laboratoire phare de la Grande Région dans le domaine de l’informatique, propose de rendre la recherche plus ouverte, plus collaborative, plus ambitieuse… en un mot, plus créative, à travers
-
Les algorithmes de Parcoursup
MathieuClaireL’objectif de la journée « Algorithmes d’aide à la décision publique » était de sensibiliser le grand public aux rôles des algorithmes d’aide à la décision publique utilisés par exemple pour l